2021. 3. 30. 13:20ㆍ노트/Python : 프로그래밍

우리의 일상에서 챗봇 고객 서비스, 이메일 스팸 탐지기, 음성 인식, 언어 번역, 주식 시장 예측 등과 상호작용하고 있습니다. 이 인공지능 상품들은 순환신경망(RNN), 롱숏-기간모델(LSTM) 그리고 게이트 순환망 (GRU)에 힘 입었습니다. 이 모델들은 시계열, 언어 패턴, 음성 패턴과 같은 순차적 데이터 예측에 최상의 예측을 가져오는 딥러닝의 중요한 가지들입니다.
회귀를 배우는 것 처럼 RNN, LSTM, GRU를 배우는 것은 쉽지 않습니다. 많은 수업에서 종종 회귀와 딥러닝 사이의 지식의 갭이 있다고 느꼈습니다. 용어의 차이 또한 지식의 갭을 만듭니다. 딥러닝으로 점프하기위해 많은 준비가 필요하며, 성공적으로 점핑한 학생들은 회귀로 쉽게 되돌아가지 않을 수 있습니다. ( 이 말장난이 마음에 들지도 모르겠네요 ) 이는 회귀와 표준 피드포워드 신경망을 잇기 위해 "회귀에 친숙한 방식으로 딥러닝 설명하기"를 작성하는데 동기부여가 되었습니다. RNN/LSTM을 배우는데 있어서, 아마도 그림(A)처럼 RNN이나 LSTM의 추상적인 다이어그램을 봤을 지도 모릅니다. 하지만 여전히 잘 모르겠지요. 장애물의 일부는 라벨링입니다. 이 다이어그램이 시계열 데이터가 정확히 어디에 있는지 정확히 이름 붙일 수 있길 바랍니다. ARIMA 모델에서는 어떻게 Yt , Yt-1 , Yt-2 , ... , 가 Yt+1을 만들어내는지 수학적인 공식으로 확인할 수 있습니다. 하지만 RNN 다이어그램으로 어떻게 이것들을 표시할까요?
당신에게 경고하건데, 이 포스팅은 긴 글입니다. 이 글은 모든 토픽에 대한 일관적인 관점들을 주기 위해서 관련된 주제들을 설명할 것입니다. 이 글을 읽은 후에는 RNN/LSTM/GRU에 대한 깊은 이해를 갖게될것이며 주가를 예측하는데 이들을 사용할 수 있을 것입니다. 읽을 가치가 있다고 생각하지 않나요? 그럼 커피한잔 하고 시작해봅시다!

주가 시계열은 계속적인 연구와 혁신을 필요로 합니다. 주가 움직임에 대한 연구를 처음 시작하는 독자들에게, 나의 "R을 활용한 알고리즘 트레이딩의 기술적 지표" 와 "주식 시장의 이상징후" 와 "주식 시장의 이상징후 탐지" 는 다르다. 글에 흥미로울 지도 모릅니다.
시계열을 설명하기 전에 세가지 광범위한 데이터 카테고리에 먼저 언급을 하는게 도움이 될것이라고 생각합니다. 세가지 데이터 카테고리는 다음과 같습니다: (1) 상관관계가 없는 데이터 (시계열 데이터와는 대조적으로) (2) 순차적인 데이터 (텍스트와 음성 스트림 데이터 포함) (3) 이미지 데이터. 딥러닝에는 각 데이터 카테고리를 해결하기위해 세가지 기본적인 변형이 있습니다. (1) 표준 피드포워드 신경망 (2) RNN/LSTM 그리고 (3) 합성곱 신경망(CNN). 각 유형에 대한 튜토리얼을 찾는 독자들에게는 (1)을 위해서는 "회귀에 친숙한 방식으로 딥러닝 설명하기"를 확인해보고, (2)를 위해서는 이번 글 " 주가예측을 위한 RNN/LSTM/GRU의 기술적 가이드"를 (3)을 위해서는 "PyTorch를 통한 딥러닝은 고문이 아닙니다.", "이미지 인식이 무엇인가요?", "오토인코더를 활용한 이상징후 탐지는 쉽게 만듭니다" 와 "이미지 노이즈 제거를 위한 합성곱 오토인코더"를 확인해보시길 추천드립니다. 요약한 글인 "데이터맨의 학습 경로 - 스킬을 쌓고, 경력을 높이세요"를 북마크해놓는 것도 좋습니다.
순차적 상관관계(Serial correlation)는 시계열 데이터의 저명한 재산입니다. 예를들어, 이번시간의 온도는 지난 시간의 온도와 관련되어있습니다. 이 순차적인 속성은 통계학자들이 1950년에 ARIMA(Auto Regressive Integrated Moving Average)모델을 발명하는데 영감을 주었습니다. 회귀모형에서 나온 ARIMA처럼 RNN/LSTM/GRU는 표준적인 딥러닝으로부터 나왔습니다.
이 글은 RNN/LSTM/GRU를 배우는데 있어서 다음의 어려움을 겪는 지점들에 관한 질문을 확실히 할 것입니다:
- 왜 전통적인 신경망 네트워크는 순차적인 데이터를 효율적으로 모델링할 수 없는것일까?
- RNN/LSTM/GRU가 3D 텐서를 입력값으로 요구한다. RNN/LSTM/GRU에 대한 일변량 주가 데이터에서 학습 데이터를 어떻게 구성해야 할까?
- RNN이 어떻게 작동하는 것일까?
- 왜 LSTM이라고 할까? 어떻게 작동하는 것일까?
- 왜 GRU라고 할까? 어떻게 작동하는 것일까?
- RNN/LSTM/GRU의 정규하는 무엇일까? 드롭아웃 테크닉은 무엇일까?
그래서 ARIMA모델의 짧은 개요로 시작하고나서, 이 질문들에 대해 순차적으로 설명하겠습니다. 이번 글은 코드 블록 뿐만 아니라 이론적인 설명을 포함합니다. 독자들은 코드 또는 이론적인 설명을 선택해서 볼 수 있으며. 전체 노트북은 이 github link 를 통해서 이용가능합니다.
(A) ARIMA 모델의 짧은 개요
ARIMA모델의 재귀적인 본성은 독자들이 RNN의 재귀적인 본성을 이해하는데 도움을 줍니다. ARIMA (Auto Regressive Integrated Moving Average) 모델은 미래를 예측하기 위해서 (a) 그 자신의 시차로 이루어진 선형 조합과 (b) 지연된 예측 오차의 선형조합에 기반을 둡니다. ARIMA 모델은 AR 항과 I 항과 MA 항을 포함합니다. ARIMA(p,d,q)모델은 세가지 항으로 특징지어집니다.
- p는 AR 항의 차수입니다.
- d는 시계열 안정성을 만들기 위한 미분 차수 입니다.
- q는 MA 항의 차수입니다.
아래는 두가지 예시입니다:

우리는 AR 항을 부분 미분으로 고려해볼 수 있습니다. AR 항에 대한 계수의 절대값은 당신이 해야할 미분의 백분율을 나타냅니다. 위에서 AR(1)은 Yt가 알려진 Yt-1 값으로 부터 얻어졌다는 것을 의미합니다. 하지만 Yt-1은 Yt-2로부터 얻어지죠. 다른말로, 데이터는 서로 상관이 있습니다. Yt는 단지 Yt-1에 의해서만 얻어지는 것도 아니고, Yt-2에 의해서만 얻어지는 것도 아닙니다. Yt에 대한 해답은 재귀적인 치환을 통해서 확인할 수 있습니다.

이것이나 이것과 같이 많은 ARIMA 튜토리얼이 이용가능합니다. 흥미로운 독자들에게 관련있는 튜토리얼을 찾아보시길 제안드립니다. 아래는 제가 $Yt = 0.8 Yt-1 - 0.2 Yt-2$ 에 대한 ARIMA(2,0,0)을 시뮬레이션 해본 것입니다.
from statsmodels.graphics.tsaplots import plot_pacf , plot_acf
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.tsa.stattools import pacf
from statsmodels.regression.linear_model import yule_walker
#from statsmodels.tsa.stattools import adfuller
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# 데이터 생성하기
ar = np.array([1, -0.8, 0.2])
ma = np.array([1])
my_simulation = ArmaProcess(ar,ma).generate_sample(nsample=100)
plt.figure(figsize=[10,5]) ; # 그림의 크기 설정
plt.plot(my_simulation, linestyle = '-', marker = 'o', color = 'b')
plt.title("Simulated Process")
plt.show()
ARIMA 모델은 자기상관함수 (ACF)와 부분자기상관함수 (PACF) 그림을 사용하여 AR 과 MA 항의 차수를 결정합니다. 그림(A.1)은 ACF가 점진적으로 0에 수렴하는 것을 보여주는 반면, PACF는 두가지 중요한 스파이크를 가지고 있음을 보여줍니다. 이 제안으로 우리는 AR2 모델 사양을 테스트할 수 있습니다. (ACF와 PACF의 규칙을 보고 싶다면, 상세한 내용은 여기를 클릭해주세요.) 그림(A.2)는 추정된 모델의 계수를 나타내며, 우리가 정한 것들과 가깝습니다.


(B) 왜 피드포워드 NN이 순차적 데이터를 효율적으로 특징화할 수 없는 것일까?
표준 피드포워드 신경망 (그림(B))는 입력 데이터 사이의 상관관계를 고려하지않고, 입력 데이터 점을 독립적으로 취급합니다. 이 제한사항은 피드포워드 NN이 순차적 데이터를 모델링하는데 적합하지 않게 만듭니다.

주식 가격 데이터를 불러오기
우리는 2013년 부터 2018년까지 일일 주가를 학습 데이터로, 2019년 데이터를 테스트 데이터로 사용할 것 입니다.
# !pip install yfinance
import pandas as pd
import yfinance as yf
AMZN = yf.download('AMZN',
start = '2013-01-01',
end = '2019-12-31',
progress = False)
all_data = AMZN[['Adj Close', 'Open', 'High','Low',"Close","Volume"]].round(2)
all_data.head(10)
print("There are "+str(all_data[:'2018'].shape[0])+" observations in the training data")
print("There are "+str(all_data['2019':].shape[0])+" observations in the test data")
all_data['Adj Close'].plot()
>>> There are 1511 observations in the training data
There are 251 observations in the test data
(C) RNN/LSTM을 위한 학습 데이터 만들기
RNN/LSTM/GRU는 강력한 ML 기법입니다. 입력값과 출력값을 모델 학습에 적합하게 만들 필요가 있는데요. 단변량 주식 가격 시계열로 부터 학습데이터를 만들어내면서 데이터 구조를 설명드리겠습니다. 여기에 유명한 데이터 구조가 있습니다: many-to-many 와 many-to-one. many-to-many가 좀 더 흥미롭십니다. 이는 미래의 많은 기간을 예측할 수 있다는 것을 의미합니다.
(C.1) Many-to-many
우리는 과거 X 일의 가격을 사용하여 미래 Y 일의 가격을 예측하는 데 관심있습니다. 설명을 위해서 5일 간의 가격으로 다음 2일의 가격을 예측해보겠습니다. 다수의 입력값 (5일의 데이터 지점)과 다수의 출력값 (2일의 데이터 지점)이 있습니다. 이 데이터 구조는 many-to-many라고 불립니다. 그림 (C.1)은 단변량 시계열 로부터 빨간색 창을 시리즈에 따라 움직여서 샘플을 만든것입니다.
각 샘플은 5가지 입력값과 2개의 출력값을 가집니다. 각 샘플의 입력값은 타임 스텝이라고 불리며, 매 타임 스텝마다 feature라고 불리는 하나의 숫자를 가집니다. 피쳐의 수는 여러개일 수 있습니다.
예를 들어서, 만약 "Adj. Close"와 "Open" 가격을 매 타임 스텝마다 함께 모델링 한다면, 두개의 피쳐가 있는것입니다. 여기에서는 "Adj.Close"만 모델링 할것이며 그래서 피쳐의 수는 하나입니다.

(C.2) Many-to-one
그림 (C.2)는 오직 하나의 출력값인 경우를 보여줍니다. 이를 many-to-one 이라고 부릅니다.

(C.3) RNN/LSTM/GRU 는 3차원의 배열을 입력값으로 요구한다.
3차원은 다음과 같습니다.
- Tensor : 하나의 텐서는 모델에 들어가는 벡터입니다.
- Time Step : 하나의 타임 스텝은 텐서에서 하나의 관측치 입니다.
- Feature : 한 feature는 그 타임 스텝에서 하나의 관측치 입니다.
위의 1차원의 배열은 3차원 배열로 변경되어야 합니다 즉,
= [# of samples, # of time steps, # of features].
이 구조는 다음을 사용해서 만들 수 있습니다. np.reshape(samples, time steps, features). 이 github link를 통해 주피터 노트북의 더 많은 예제를 제공하겠습니다.
(C.3) 입력값과 출력값 데이터를 위한 코드
당신이 입력값과 출력값의 데이터 구조에 대해 명백한 생각을 가지게 되었길 희망합니다. 아래는 그림 (C.1) 과 (C.2)의 입력값과 출력값을 생성하기 위한 코드입니다. 트레이닝 데이터에는 1,504개의 행 또는 샘플이 있습니다. 또 테스트 데이터에는 249개의 샘플이 있습니다.
def ts_train_test(all_data, time_steps, for_periods):
"""
input:
data: dataframe with dates and price data
output:
X_train, y_train: data from 2013/1/1-2018-12/31
X_test : data from 2019 -
time_steps: # of the input time steps
for_periods: # of the output time steps
"""
# create training and test set
ts_train = all_data[:'2018'].iloc[:,0:1].values
ts_test = all_data['2019':].iloc[:,0:1].values
ts_train_len = len(ts_train)
ts_test_len = len(ts_test)
# create training data of s samples and t time steps
X_train = []
y_train = []
y_train_stacked = []
for i in range(time_steps, ts_train_len - 1):
X_train.append(ts_train[i-time_steps:i,0])
y_train.append(ts_train[i:i+for_periods,0])
X_train, y_train = np.array(X_train), np.array(y_train)
# Reshapng X_train for efficient modelling
X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1],1))
# Preparing to creat X_test
inputs = pd.concat((all_data["Adj Close"][:'2018'], all_data["Adj Close"]['2019':]), axis=0).values
inputs = inputs[len(inputs)-len(ts_test) - time_steps:]
inputs = inputs.reshape(-1,1)
X_test = []
for i in range(time_steps, ts_test_len+ time_steps- for_periods):
X_test.append(inputs[i-time_steps:i,0])
X_test = np.array(X_test)
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1],1))
return X_train, y_train, X_test
X_train, y_train, X_test = ts_train_test(all_data,5,2)
X_train.shape[0], X_train.shape[1]
>>> (1505, 5)X_train, Y_train , X_test를 데이터 프레임으로 바꾸고 아래에 출력했습니다. 그림 (C.1) - (C.3)과 비슷한 것을 보셨길 제안드립니다.
# Convert the 3D shape of X_train to a data frame so we can see:
X_train_see = pd.DataFrame(np.reshape(X_train, (X_train.shape[0], X_train.shape[1])))
y_train_see = pd.DataFrame(y_train)
pd.concat([X_train_see, y_train_see], axis = 1)
# Convert the 3D shape of X_test to a data frame so we can see:
X_test_see = pd.DataFrame(np.reshape(X_test, (X_test.shape[0], X_test.shape[1])))
pd.DataFrame(X_test_see)
print("There are " + str(X_train.shape[0]) + " samples in the training data")
print("There are " + str(X_test.shape[0]) + " samples in the test data")
>>> There are 1505 samples in the training data
There are 249 samples in the test data
(D) 어떻게 RNN이 작동하나요?
그림 (D.1)은 RNN을 나타내며, 완전 신경망으로 그것을 펼쳤습니다. 그림 (B)의 피드포워드 신경망과는 매우 다르다는 것을 알았나요? RNN은 순환신경망이라고 불립니다. 왜냐하면 이 모델은 이전의 계산으로부터 나온 결과를 고려하여 같은 일을 매 샘플마다 반복해서 수행하기 때문입니다. 또한 RNN을 한 타임 스텝에서 다른 타임 스텝으로 정보가 전달되는 "memory"를 가졌다고 생각할 수 있습니다. 이론적으로 RNN은 많은 타임 스텝의 긴 샘플을 다룹니다. 이는 주가에 적합합니다. 왜냐하면 정보가 한 시점의 주가로부터 다음 시점의 주가로 흘러가기 때문입니다. 이는 수일 전, 즉 작년 같은 날의 가격 정보가 오늘날 가격에 여전히 남아있다는 것을 의미합니다. 하지만, 긴 샘플은 계산을 매우 시간 소비하도록 만들고 불필요할지도 모릅니다. 우리의 경우 X_train의 각 샘플 (행)에 5개의 입력값과 2개의 출력값을 가지고 있습니다. 그래서 다이어그램은 5개의 타임 스텝 X_t-4, X_t-3, X_t-2, X_t-1, X_t 과 두개의 타임 스텝 y_t+1, y_t+2을 가지고 있습니다. 네트워크는 5개의 은닉층을 가지고 있으며 이는 5개의 입력층이 있기 때문입니다.


Step-by-step 설명:
- Xt-4에서 Xt: 샘플의 타임스텝, 예를들어 그림(C.3)의 257.31, 258.48, 259.15, 268.46, 266.38 , 입니다. 각 타임 스텝은 feature 수의 벡터입니다. 우리의 케이스에서는 하나의 feature를 가졌기에 각 xt-4에서 xt의 차원은 1입니다.
- ht-4 에서 ht: t-1에서 t까지 타임 스텝의 은닉 상태입니다. 이것은 네트워크의 "메모리"입니다. 각각은 이전의 은닉상태에 기반하여 계산되며, 현재 스텝의 입력값은 다음과 같습니다:

- 첫번째 은닉 상태 h0는 일반적으로 0으로 초기화 됩니다.
- 활성화 함수 f(.)는 tanh 나 ReLU (Rectified Linear Unit) 입니다. 아이디어는 로지스틱 회귀에서 쓰이는 로짓 함수와 비슷합니다. 로지스틱 회귀에서 로짓 함수가 왜 필요할까요? 선형 회귀 Y = XB+ e, 에서는 독립변수 X 와 예측값 Y가 음수에서 양수 무한대의 어떤 값이든 가질 수 있습니다. 로지스특 회귀가 확률에 대한 것이기 때문에, 출력값을 0과 1 사이의 값으로 변형시킬 필요가 있습니다. 그렇지 않으면 출력 값이 음이나 양의 무한대로 발산할 수도 있습니다. 이런 현상을 예방하기 위해서, 여기 tanh나 ReLU 함수가 0과 1사이의 출력값으로 변형하기 위해 사용됩니다.

- bt : 노이즈 항
- yt+1 , yt+2 : 은 출력값입니다. 은닉층과 tanh 활성화 함수의 행렬 곱입니다.
- keras의 simpleRNN의 디폴트값은 아래와 같습니다.

- U, W, V: 는 행렬의 파라미터입니다. 모든 스텝에서 같은 행렬이 반복적으로 사용됩니다. 이는 다른 입력값으로 같은 작업을 수행한다는 것을 나타냅니다. 행렬의 차수은 어떻게 될까요? 이는 사소한 질문이 아닙니다. (D.1)에서 설명하겠습니다.
(D.1) keras의 RNN/LSTM/GRU 레이어에서 "Units"이란 무엇일까요?
이는 아마도 가장 혼란스러운 질문일것입니다. 공식적인 keras'의 "units"에 대한 설명은 "출력값 공간의 차원성"이라고 합니다. 저는 여전히 이해하기 쉽지 않네요. ( 가끔 인터넷의 소스코드는 이 값을 표본의 시간 단계 수와 혼동합니다. ) 나는 "units"를 "잠재 차원(latent dimension)" 또는 "latent_dim"이라고 부르는 것이 더 낫다고 느낌니다. (여기 keras' 코드에서 사용되었듯이) 이렇게 이름을 바꾸면 적어도 차원성이 내부적인 것이며 외부 매개변수와 관련이 없음을 의미하게 됩니다.
은닉층의 차원이 "units"입니다. 은닉층이기 때문에, 은닉층의 뉴런의 수를 구체화할 필요가 있습니다. 은닉층의 차원은 어떤 수든 될 수 있습니다. 은닉층의 차원은 모든 과거 정보의 메모리를 유지하기 위해서 RNN의 성능을 결정합니다. 보통 작은 수가 아니며, 관습적으로 32,64,128과 같은 32의 배수가 됩니다.

그림 (D.5)는 은닉층의 차원을 설명합니다. 각 xt-4에서 xt까지의 타임 스텝은 feature 수의 벡터입니다. 우리의 경우 하나의 feature이어서, 각 xt-4에서 xt의 차원은 1입니다. 즉 , Nx = 1 입니다. Nh는 은닉 층의 차원입니다. 만약 Nh = 32 라면, 행렬 U의 매개변수는 (32 x 1)이 됩니다. U와 xt의 행렬 곱(dot product)은 (32 x 1 ) x ( 1 x 1 ) = (32 x 1) 차원이 됩니다.
마찬가지로, 행렬 W의 매개변수는 (32 x 32)여서, W와 ht-1의 행렬 곱은(dot product) (32 x 32) x (32 x 1 ) = (32 x 1) 입니다. 노이즈 벡터는 그래서 (32 x 1 ) vector가 되어야 합니다.
(D.2) Simple RNN 모델 구성하기
def simple_rnn_model(X_train, y_train, X_test):
"""
create single layer rnn model trained on X_train and y_train
and make predictions on the X_test data
"""
# create a model
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN
my_rnn_model = Sequential()
my_rnn_model.add(SimpleRNN(32, return_sequences = True))
my_rnn_model.add(SimpleRNN(32))
my_rnn_model.add(Dense(2)) # The time step of the output
my_rnn_model.compile(optimizer = 'rmsprop', loss = 'mean_squared_error')
# fit the RNN model
my_rnn_model.fit(X_train,y_train, epochs = 100, batch_size = 150, verbose = 0)
# Finalizing predictions
rnn_predictions = my_rnn_model.predict(X_test)
return my_rnn_model, rnn_predictions
my_rnn_model, rnn_predictions = simple_rnn_model(X_train, y_train, X_test)
rnn_predictions[1:10]
def actual_pred_plot(preds):
"""
Plot the actual vs predition
"""
actual_pred = pd.DataFrame(columns = ['Adj. Close', 'prediction'])
actual_pred['Adj. Close'] = all_data.loc['2019':,'Adj Close'][0:len(preds)]
actual_pred['prediction'] = preds[:,0]
from keras.metrics import MeanSquaredError
m = MeanSquaredError()
m.update_state(np.array(actual_pred['Adj. Close']), np.array(actual_pred['prediction']))
return (m.result().numpy(), actual_pred.plot())
actual_pred_plot(rnn_predictions)
>>> (3070557.0, <matplotlib.axes._subplots.AxesSubplot at 0x20e8c738490>)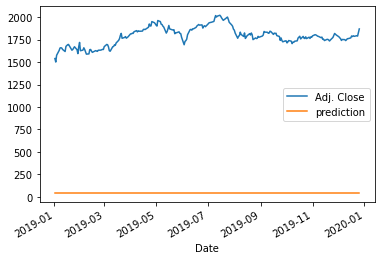
모델 예측결과가 terrible 합니다! 왜그런지 아시나요? 입력 데이터가 정규화되었지 않기 때문입니다. (D.2)에서 입력데이터를 정규화할것입니다. 핵심 교훈은 : RNN/LSTM/GRU에서 정규화(normalization)는 필수적이라는 것입니다.
함수 actual_pred_plot()는 또한 mean square error를 계산합니다. 결과는 (저의 경우) 3,070,557이 나왔습니다.
몇개의 simpleRNN 층을 추가할 수 있으나, 여기서는 생략하겠습니다. 구조를 달리해서 성능을 실험해볼 수도 있겠습니다.
(D.3) RNN/LSTM/GRU에는 정규화된 데이터가 필요합니다.
아래의 코드 (Line 16-19)는 입력 데이터를 정규화 하였습니다. 당신의 모델을 학습하기 위해 데이터를 표준화 할때, 오직 학습 데이터만 스케일 변환(scaler transformation)에 사용된다는 점을 기억하세요. 그리고 나서, 스케일러는 테스트 입력 데이터를 변형하기위해 사용됩니다. 내가 "커리어에 손실을 입힐 수 있는 치명적인 모델링 실수 방지하기" 에서 언급했듯이, x_train과 x_test를 독립적으로 스케일링 하지 마세요. Line 72는 scaler를 적용하여 스케일 예측을 원래 스케일로 변환합니다. 예측 성능은 아래 그래프에서 보여지듯이 더욱 좋아집니다. MSE는 (저의 경우 6047) 입니다.
def ts_train_test_normalize(all_data, time_steps, for_periods):
"""
input:
data: dataframe with dates and price data
output:
X_train, y_train: data from 2013/1/1-2018/12/31
X_test : data from 2019-
sc : insantiated MinMaxScaler object fit to the training data
"""
# create training and test set
ts_train = all_data[:'2018'].iloc[:,0:1].values
ts_test = all_data['2019':].iloc[:,0:1].values
ts_train_len = len(ts_train)
ts_test_len = len(ts_test)
# scale the data
from sklearn.preprocessing import MinMaxScaler
sc = MinMaxScaler(feature_range=(0,1))
ts_train_scaled = sc.fit_transform(ts_train)
# create training data of s samples and t time steps
X_train = []
y_train = []
for i in range(time_steps, ts_train_len-1):
X_train.append(ts_train_scaled[i-time_steps:i, 0])
y_train.append(ts_train_scaled[i:i+for_periods, 0])
X_train, y_train = np.array(X_train), np.array(y_train)
# Reshaping X_train for efficient modelling
X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1 ))
inputs = pd.concat((all_data["Adj Close"][:'2018'], all_data["Adj Close"]['2019':]), axis=0).values
inputs = inputs[len(inputs)-len(ts_test)-time_steps:]
inputs = inputs.reshape(-1,1)
inputs = sc.transform(inputs)
# Preparing X_test
X_test = []
for i in range(time_steps, ts_test_len + time_steps - for_periods):
X_test.append(inputs[i-time_steps:i,0])
X_test = np.array(X_test)
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
return X_train, y_train , X_test, sc
def simple_rnn_model(X_train, y_train, X_test, sc):
"""
create single layer rnn model trained on X_train and y_train
and make predictions on the X_test data
"""
# create a model
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN
my_rnn_model = Sequential()
my_rnn_model.add(SimpleRNN(32, return_sequences = True))
my_rnn_model.add(SimpleRNN(32))
my_rnn_model.add(Dense(2)) # The time step of the output
my_rnn_model.compile(optimizer = 'rmsprop', loss = 'mean_squared_error')
# fit the RNN model
my_rnn_model.fit(X_train,y_train, epochs = 100, batch_size = 150, verbose = 0)
# Finalizing predictions
rnn_predictions = my_rnn_model.predict(X_test)
from sklearn.preprocessing import MinMaxScaler
rnn_predictions = sc.inverse_transform(rnn_predictions)
return my_rnn_model, rnn_predictions
X_train, y_train, X_test, sc = ts_train_test_normalize(all_data, 5,2)
my_rnn_model, rnn_predictions_2 = simple_rnn_model(X_train, y_train, X_test, sc)
rnn_predictions_2[1:10]
actual_pred_plot(rnn_predictions_2)
>>> (6047.518, <matplotlib.axes._subplots.AxesSubplot at 0x1abbe49cee0>)
(E) 왜 LSTM/GRU가 필요할까요?
RNN의 옵티마이저는 최적 값을 찾기 위해 손실함수의 일차 미분 값을 얻게됩니다. RNN가 재귀적(recursive)이기 때문에, 일차 미분값은 계속해서 수가 점점 더 작아집니다. 그래서 결국 소멸하게 됩니다. 이것을 기울기 소실 (gradient vanishing) 이라고 부릅니다. 이 확실한 수학적 프로세스는 RNN을 과거 기억을 유지하기에 좋은 선택이 아니도록 만듭니다. 우리는 정보가 빠르게 소멸되지 않는 순환 구조가 필요합니다. 이것이 LSTM과 GRU의 모티브입니다. (최적화 과정에 친숙하지 않은 독자들에게: 손실함수는 실제값과 예측값 사이의 오차를 측정하는 척도가 됩니다. 옵티마이저는 최소 오차를 추구하는 뉴런의 가중치를 변경하는 알고리즘입니다. 유명한 옵티마이저로는 확률적 경사 하강 (Stochastic Gradient Descent (SGD)) 가 있습니다. "Random Forest, Gradient Boosting, Regularization, H2O.ai에 관한 강의 노트" 글은 SGD에 대한 상세한 설명을 제공합니다. 위 코드는 옵티마이저로 RMSprop, Root Mean Square Propogation, 로 지정했습니다.
(F) 왜 LSTM (Long Short-Term Memory) 일까요?
Hochreiter 와 Schmidhuber (1997)은 좀 더 긴 시간동안 RNN의 메모리를 유지하기 위해 LSTM 구조를 제안했습니다. 이 논문은 추가적인 게이트, 입력 및 출력 게이트를 도입함으로써 기울기 소실 (혹은 기울기 폭발) 문제를 해결했습니다. 이 추가적인 게이트는 무슨 정보가 보존되어야하고 어떤 것을 잊어버릴 지를 가능하게 하면서 기울기에 대해 더 잘 컨트롤 할 수 있습니다. 이 게이트는 제한된 정보 또는 모든 정보를 통과하기 위해 출력값 [0,1]을 가지는 시그모이드 함수입니다. 0 값은 정보를 완전히 필터링 하는 것을 의미하는 반면, 1 값은 정보를 완전히 지나가도록 하는 것을 의미합니다. 이 구조는 더 긴 메모리를 만들기위해 짧은 기간의 메모리 프로세스를 사용하기 때문에 Long Short-Term Memory라고 불립니다. (그래서 "Long Short-Term Memory"를 "Long-Short Term Memory"로 잘못 적지 않도록 합시다)
어떻게 LSTM이 메모리를 장기간동안 유지할 수 있을까요? LSTM은 은닉층 외에도 오래된 정보를 곧 사라지는 것으로 부터 예방하기 위하여 cell state라고 불리는 고유의 레이어를 가지고 있습니다. 보통 Ct라고 적습니다. 우리의 주식 가격 예시에서, 금요일날 가격은 이전의 금요일의 가격이나 혹은 작년의 같은날에 영향을 받을지도 모릅니다. RNN은 작년의 같은 날의 정보를 유지할 수 없을지도 모르지만, LSTM은 이론적으로 이를 유지하도록 구성되었습니다.
(F.1) 기울기 소실 문제에 대한 수학적 설명
이미 이에 대한 아이디어를 알고 있다면 수학적 설명을 스킵하고 (F.2)로 자유롭게 넘어가세요. 우리는 수학적으로 심플하게 하기 위해서 t시점에 은닉층 ht를 가졌다고 가정하고, bias bt 와 입력값 xt 항을 제거해보겠습니다. :

일차 미분을 취하여 다음의 등식을 얻었습니다. 동그라미친 계수 벡터가 핵심입니다. 이는 기하급수적으로 0으로 소멸하거나 기하급수적으로 무한대로 폭팔할것입니다.
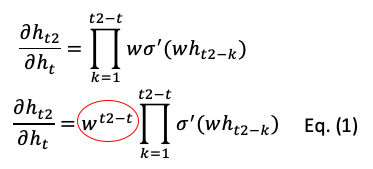
이 문제를 해결하기 위해, LSTM은 cell state st를 추가했습니다. 미분 방정식은 다음과 같습니다. :

여기 vt는 forget gate의 입력값입니다. 여기에는 변수 w의 소멸이 없기 때문에, 빠르게 소멸되지 않습니다. 그러나 Eq.(2) 또한 시그모이드 함수를 가져서 행렬 곱이 소멸되지 않냐고 물어볼지도 모릅니다. 정확합니다. LSTM도 여전히 기울기 소실 문제를 가지고 있습니다. 하지만 Eq.(1) 만큼 빠르진 않습니다.
(F.2) LSTM의 구조
많은 논문들이 LSTM의 내부 구조에 대해 증명하기만 해서, 어떻게 시스템이 작동하는지에 대해 당신을 혼란스럽게 할지도 모릅니다. 그래서 나는 그림(F.2)에 LSTM의 완전한 그림을 그렸습니다. 전체 시스템을 당신에게 보여주기 위해 그림(D.2)에 있는 RNN의 구조와 비슷합니다.

이 LSTM은 4개의 구성요소를 가지고 있습니다: input gates, forget gate, cell state, output gate.
- Input Gate: 목표는 새로운 정보 xt 를 가져오는 것입니다. 여기에 새로운 정보를 가져오는 두개의 함수가 있습니다. : rt 와 dt 입니다. rt는 이전의 은닉 벡터 ht-1 을 새로운 정보 xt 에 결합합니다. 즉, [ht-1, xt] , 그리고 새로운 행렬Wr 에 곱하고, 노이즈 벡터 br을 더합니다. dt도 비슷하게 수행합니다. 그리고 rt 와 dt 는 요소별로 곱하여 cell state ct 에 가져오게 됩니다.

- Forget Gate: forget gate ft는 input gate의 rt와 비슷하게 생겼습니다. 이는 메모리에 어떤 값이 유지될지 제한 선을 통제합니다.

- Cell State: 이전의 cell state Ct-1 과 forget gate ft 사이의 요소별 곱셈을 계산합니다. 그리고 나서, input gate rt 와 dt를 곱한 결과를 더합니다.

- Output gate: 여기 ot 는 t 시점의 output gate입니다. 그리고 W0 과 b0 는 output gate의 가중치와 편향입니다. 은닉층 ht 는 다음 시점으로 이동하거나 yt 로 출력됩니다. 다음 코드의 Line 12 에서, yt 는 다른 ht 에 tanh를 적용하여 얻어집니다. output gate ot 가 output yt 가 아니라는 점에 주목해주세요. 이는 단순히 output을 컨트롤하기위한 "gate" 입니다.

def LSTM_model(X_train, y_train, X_test, sc):
# create a model
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN, GRU, LSTM
from keras.optimizers import SGD
# The LSTM architecture
my_LSTM_model = Sequential()
my_LSTM_model.add(LSTM(units = 50,
return_sequences = True,
input_shape = (X_train.shape[1],1),
activation = 'tanh'))
my_LSTM_model.add(LSTM(units = 50, activation = 'tanh'))
my_LSTM_model.add(Dense(units=2))
# Compiling
my_LSTM_model.compile(optimizer = SGD(lr = 0.01, decay = 1e-7,
momentum = 0.9, nesterov = False),
loss = 'mean_squared_error')
# Fitting to the training set
my_LSTM_model.fit(X_train, y_train, epochs = 50, batch_size = 150, verbose = 0)
LSTM_prediction = my_LSTM_model.predict(X_test)
LSTM_prediction = sc.inverse_transform(LSTM_prediction)
return my_LSTM_model, LSTM_prediciton
my_LSTM_model, LSTM_prediction = LSTM_model(X_train, y_train, X_test, sc)
LSTM_prediction[1:10]
actual_pred_plot(LSTM_prediction)
>>> (2442.6787, <matplotlib.axes._subplots.AxesSubplot at 0x1abc7dbf970>)
(F.3) Regularization을 적용한 LSTM
오버피팅은 머신러닝에서 중요한 부분입니다. 당신이 학습 데이터를 모델에 트레이닝 하고, 테스트 데이터에 적용할 때, 테스트 데이터의 정확도는 보통 학습 데이터의 정확도 보다 낮습니다. 우리는 모델이 학습데이터의 노이즈를 포함하여, 학습 데이터에 너무 잘 적합되었기 때문이라고 알고 있습니다. 그러나 만약 오버피팅으로 테스트 데이터에 대한 예측의 효율성이 떨어진다면 어떤 문제가 발생할까요? 왜 학자들과 실무자들이 수년간 작업을 통해 오버피팅을 피하려고 할까요?
진짜 문제는 오버피팅이 당신의 모델의 비효율적으로 만들 뿐만아니라, 당신의 예측을 매우 잘못된 것으로 만든다는 것입니다. 당신으 최종 모델이 10개의 변수를 가지고 있다고 가정해봅시다. 그중 8개는 진짜 패턴을 포착하였고 나머지 2 변수는 노이즈입니다. 다른 말로 2개의 변수가 노이즈에 과적합되었고, 이는 쓸모없는 것입니다. 당신의 10개 변수 모델에 새로운 데이터를 예측하려고 한다고 가정해봅시다. 그리고 이 두개 변수에 대한 새로운 값이 꽤 크다고 해봅시다. 무슨 일이 벌어질 지 추측해볼까요? 당신의 예측은 두 변수와 새로운 데이터의 큰 값 때문에 매우 잘못될 것입니다. 그래서 오버피팅은 당신의 모델을 비효율적으로 만들 뿐만아니라, 예측을 잘 못된 것으로 만듭니다.
딥러닝은 드롭아웃 기술(dropout technique) 을 사용하여 오버피팅을 컨트롤합니다. 드롭아웃 기법은 각 실행 동안에 레이어의 몇몇 신경망들을 임의로 드롭하거나 비활성화합니다. 몇몇 가중치를 0으로 설정하는 것과 같습니다. 따라서 각 실행에서 모델을 최적화 하기 위해 모델은 약간의 다른 구조를 보입니다. 상세한 설명을 위해서는 "친절한 방식으로- 회귀의 딥러닝 설명하기"를 보세요.
RNN/LSTM/GRU에서 드롭아웃을 다루는것 또한 연구 주제입니다. 피드포워드 신경망에서 같은 층의 뉴런들 사이에 연결성이 없기 때문에 뉴런을 드롭하는 것은 더욱 쉽습니다. 그러나, RNN/LSTM/GRU에서 시점마다 드롭하는 것은 시간에 따라 정보력이 있는 신호를 전달하는 능력에 피해를 줍니다. 해결책은 무엇일까요? Pham et al.(2013)은 시퀀스 위치 사이가 아니라 깊은 RNN의 레이어 사이에서만 드롭아웃을 적용하기를 제안했습니다. Gal and Ghahramani (2015)는 드롭아웃을 RNN의 모든 구성요소 (recurrent 와 비-recurrent 둘다) 에 적용하기를 제안했습니다. 하지만 시간 단계마다 같은 드롭아웃 마스크를 유지하도록 해야합니다. 이 논문이 좋은 리뷰를 제공합니다.
def LSTM_model_regularization(X_train, y_train, X_test, sc):
# create a model
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN, GRU, LSTM, Dropout
from keras.optimizers import SGD
# LSTM 아키텍쳐
my_LSTM_model = Sequential()
my_LSTM_model.add(LSTM(units = 50,
return_sequences = True,
input_shape = (X_train.shape[1],1),
activation = 'tanh'))
my_LSTM_model.add(LSTM(units = 50, activation = 'tanh'))
my_LSTM_model.add(Dropout(0.2))
my_LSTM_model.add(Dense(units=2))
# Compiling
my_LSTM_model.compile(optimizer = SGD(lr = 0.01, decay = 1e-7,
momentum = 0.9, nesterov = False),
loss = 'mean_squared_error')
# Fitting to the training set
my_LSTM_model.fit(X_train, y_train, epochs = 50, batch_size = 150, verbose = 0)
LSTM_prediction = my_LSTM_model.predict(X_test)
LSTM_prediction = sc.inverse_transform(LSTM_prediction)
return my_LSTM_model, LSTM_prediction
my_LSTM_model, LSTM_prediction = LSTM_model_regularization(X_train, y_train, X_test, sc)
LSTM_prediction[1:10]
actual_pred_plot(LSTM_prediction)
>>> (3859.3274, <matplotlib.axes._subplots.AxesSubplot at 0x1abba10d730>)
MSE는 (저의 경우) 3859 입니다.
(G) GRU (Gated Recurrent Units)
GRU는 Cho et al. (2014)가 RNN 및 LSTM과 함께 개발했습니다. 재귀 네트워크의 더 많은 변형이 계속해서 나타날 것으로 예상되는데요. GRU 또한 기울기 소실 문제(vanishing gradient problem) 를 해결하는 것을 목적으로 합니다. GRU는 LSTM처럼 cell state와 output gate를 가지고 있지 않습니다. 그래서 LSTM보다 더 적은 파라미터를 가집니다. GRU는 은닉층을 정보를 전달하기 위해 사용합니다. GRU는 이 두가지 게이트를 reset gate와 update gate라고 불릅니다. 하나씩 설명해보겠습니다.
(G.1) GRU 구조
GRU의 매개변수는 Wr, Wz, W를 포함합니다. 리셋 신호 rt 는 만약 이전 은닉층이 무시 될지 말지를 결정하는 반면, 업데이트 신호 zt 는 은닉층 ht 가 새로운 은닉 상태 hat(ht)에 업데이트 될지 말지를 결정합니다.

- Reset Gate : 이 게이트는 LSTM에서 input gate와 forget gate가 달성한 것을 해냅니다. 게이트 rt 는 이전 은닉 상태가 무시될지 말지를 결정합니다. 게이트 zt는 update gate에서 hat(ht)를 반영할 비율을 결정합니다. Wz 와 Wr 은 학습될 가중치 매개변수이며, bz 와 br 은 노이즈 벡터입니다.

- Update Gate: (Part1) 이 부분은 rt 와 ht-1 을 곱합니다. 이 곱셈은 얼마나 많은 양의 ht-1이 유지되거나 무시될지를 의미합니다. 이는 ht 의 업데이트에 사용되기 위한 일시적인 hat(ht)를 만들어냅니다. Wh 와 bh 는 가중치 파라미터와 노이즈 벡터 입니다.

- Update Gate: (Part 2) 이 부분은 가중치 zt 에 따라 ht-1과 hat(ht) 사이의 가중 평균을 계산합니다. 만약 zt 가 0에 가깝다면 과거 정보는 매우 적게 기여할 것이고 새로운 정보가 더 많이 기여할 것입니다.

(G.2) GRU 코드
def GRU_model(X_train, y_train, X_test, sc):
# create a model
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN, GRU
from keras.optimizers import SGD
# The GRU architecture
my_GRU_model = Sequential()
my_GRU_model.add(GRU(units = 50,
return_sequences = True,
input_shape = (X_train.shape[1],1),
activation = 'tanh'))
my_GRU_model.add(GRU(units = 50,
activation = 'tanh'))
my_GRU_model.add(Dense(units = 2))
# Compiling the RNN
my_GRU_model.compile(optimizer = SGD(lr = 0.01, decay = 1e-7,
momentum = 0.9, nesterov = False),
loss = 'mean_squared_error')
# Fitting to the trainig set
my_GRU_model.fit(X_train, y_train, epochs = 50, batch_size = 150, verbose = 0)
GRU_prediction = my_GRU_model.predict(X_test)
GRU_prediction = sc.inverse_transform(GRU_prediction)
return my_GRU_model, GRU_prediction
my_GRU_model, GRU_prediction = GRU_model(X_train, y_train, X_test, sc)
GRU_prediction[1:10]
actual_pred_plot(GRU_prediction)
>>> (1234.0574, <matplotlib.axes._subplots.AxesSubplot at 0x1abd17ac3a0>)
(G.1) Regularization을 적용한 GRU
다음 코드는 GRU에 dropout 기술을 적용했습니다. 위에서 설명한 것과 매우 비슷하기 때문에, 더이상 설명을 많이 하지 않겠습니다. MSE는 (저의 경우) 1706 입니다.
def GRU_model_regularization(X_train, y_train, X_test, sc):
"""
create a GRU model trained on X_train and y_train
and make predictions on the X_test data
"""
# create a model
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN, GRU, Dropout
from keras.optimizers import SGD
# The GRU architecture
my_GRU_model = Sequential()
my_GRU_model.add(GRU(units = 50,
return_sequences = True,
input_shape = (X_train.shape[1],1),
activation = 'tanh'))
my_GRU_model.add(GRU(units = 50,
activation = 'tanh'))
my_GRU_model.add(Dropout(0.2))
my_GRU_model.add(Dense(units = 2))
# Compiling the RNN
my_GRU_model.compile(optimizer = SGD(lr = 0.01, decay = 1e-7,
momentum = 0.9, nesterov = False),
loss = 'mean_squared_error')
# Fitting to the trainig set
my_GRU_model.fit(X_train, y_train, epochs = 50, batch_size = 150, verbose = 0)
GRU_prediction = my_GRU_model.predict(X_test)
GRU_prediction = sc.inverse_transform(GRU_prediction)
return my_GRU_model, GRU_prediction
my_GRU_model, GRU_prediction = GRU_model_regularization(X_train, y_train, X_test, sc)
GRU_prediction[1:10]
actual_pred_plot(GRU_prediction)
>>> (1706.2977, <matplotlib.axes._subplots.AxesSubplot at 0x1abc99ec3a0>)

이것이 긴 글이라는 것을 이해합니다. 지금까지 잘 따라왔다면, 축하드립니다! 전체 노트북은 여기 깃헙 링크에서 이용가능합니다. 확인해보세요!
원문
A Technical Guide on RNN/LSTM/GRU for Stock Price Prediction
In our daily lives we interact with chatbot customer services, e-mail spam detections, voice recognition, language translation, or stock…
medium.com
'노트 > Python : 프로그래밍' 카테고리의 다른 글
| [Attention] 컴퓨터 비젼에서의 어텐션 기법 (번역) (0) | 2021.08.02 |
|---|---|
| [딥러닝 기초] 신경망 코딩하기 (텐서플로우, 파이토치 활용) (0) | 2021.05.19 |
| Keras와 OpenCV를 활용하여 웹캠으로 실시간 나이, 성별, 감정 예측 (번역) (3) | 2021.03.26 |
| [시계열] 케라스에서 Luong 어텐션을 활용한 seq2seq2 LSTM 모델 만들기 (번역) (4) | 2020.12.16 |
| [시계열] Time Series에 대한 머신러닝(ML) 접근 (2) | 2020.12.12 |