2022. 12. 10. 14:44ㆍ노트/Data Science : 데이터과학
목차 :
- 이항 분포 (Binomial Distribution)
- 연속 Uniform 분포 (Continuous Uniform Distribution)
- 정규 분포 (Normal Distribution)
- 중심 극한 정리 (Central Limit Theorem (CLT))
- 점 추정 (Point estimation)
- 신뢰 구간 (Confidence Interval)
이항 분포 (Binomial Distribution)
문제 설명
Lavista 박물관의 방문객중 80%는 박물관 내의 기념품 점에서 결국 기념품을 구매합니다. 다음주 일요일날, 임의의 10명의 표본이 선택되었습니다. :
- 모든 사람들이 기념품 점에서 결국 기념품을 구매할 확률을 구하세요.
- 최대 7명의 방문객들이 기념품 점에서 기념품을 구매할 확률을 구하세요.
이항 분포의 가정을 만족하는지 아닌지 확인해봅시다.
여기에는 매 시도 때마다, 가능한 결과가 2가지 (성공 또는 실패) 가 있습니다. - 방문객이 기념품을 사거나 / 사지 않거나 (yes or no). 시행 수 (The number of trials (n)) 는 고정되었습니다. - 샘플에는 10명의 방문객들이 있습니다. 각 시행은 다른 시행들과 독립적입니다. - 방문객들의 사는 행위는 독립적이라고 가정하는 것이 합리적일 수 있습니다. 성공할 확률 (p) 는 각 시행마다 동일합니다. - 각 방문객들마다 성공할 확률은 0.8 입니다.
Import Libraries
import pandas as pd # 데이터 핸들링과 분석에 사용되는 라이브러리
import numpy as np # 배열 (arrays) 을 핸들링할 때 사용되는 라이브러리
import matplotlib.pyplot as plt # 그림과 시각화를 위한 라이브러리
import seaborn as sns # 시각화를 위한 라이브러리
%matplotlib inline
import scipy.stats as stats # 다수의 통계 분포 뿐만 아니라, 통계적 함수를 포함한 라이브러리# 경고무시
import warnings
warnings.filterwarnings('ignore')방문자들의 확률 분포를 측정해보자
# 표본의 크기를 선언하자. n : 임의로 선택된 방문객들의 수 를 변수로 표현한 것이다.
n = 10
# p : 성공 확률을 선언하자, 즉, 방문객이 기념품 점에서 구매할 확률이다.
p = 0.8
# numpy array로 선택된 방문객들의 가능한 수를 선언하자.
k = np.arange(0, 11)
k
>>> array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])# import the required function
from scipy.stats import binom
binomial = binom.pmf(k = k, n = n, p = p)
binomial
>>> array([1.02400000e-07, 4.09600000e-06, 7.37280000e-05, 7.86432000e-04,
5.50502400e-03, 2.64241152e-02, 8.80803840e-02, 2.01326592e-01,
3.01989888e-01, 2.68435456e-01, 1.07374182e-01])다른 성공의 수마다 이항분포의 확률을 배열의 형태로 확인할 수 있다. 다음 그림으로 시각화 해보자.
plt.bar(k, binomial) # bar plot을 만들자
plt.title("Binomial: n = %i , p = %.2f" % (n, p), fontsize = 15)
plt.xlabel("Number of Successes")
plt.ylabel("Probability of Successes")
plt.show()
binomial 배열의 마지막 원소는 성공이 10번이 될 확률을 의미한다. 이 뜻은, 모든 임의로 선택된 10명의 방문객들 모두 기념품 점에서 기념품을 구매한다는 것을 의미한다.
binomial[10]
>>> 0.10737418240000006위 확률에서 볼 수 있듯, 정확히 10번의 성공이 있을 확률은 대략 ~ 0.11 정도이다.
이제, 우리는 최대 7번의 성공이 있을 확률에 관심이 있다. 이것은 10명의 임의로 선택된 방문객들 중에서 최대 7명의 방문객들이 기념품 점에서 기념품을 구매할지에 대한 확률이다.
여기서, P(X<=7) 에 대한 확률을 구할 필요가있다. CDF 는 누적 확률 분포를 구하는데 사용된다
# 확률 분포를 그려보자.
# 계산 값들을 더 잘 시각화 하기위해 여기 분포를 그려볼 것이다.
barl = plt.bar(k, binomial)
plt.title("Binomial: n=%i , p = %.2f" % (n,p) , fontsize = 15)
plt.xlabel("Number of Success")
plt.ylabel("Probability of Successes")
for i in range(0, 8):
barl[i].set_color("r")
plt.show()
위 그래프에서 빨간색 지역이 P(X <= 7) 로 표현 되었다. 임의로 선택된 방문객 10명 중 들을 최대 7명이 기념품 샵에서 기념품을 살 확률을 구해보자. 우리는 binom.cdf()를 사용할 것이다
binom.cdf(k = 7, n = n, p = p)
>>> 0.32220047359999987결론 :
모든 방문객들이 결국 기념품 샵에서 기념품을 구매할 확률은 10.74% 정도이고,
임의로 선택된 10명 중 최대 7명의 방문객들이 기념품 샵에서 기념품을 구매할 확률은 32.22% 정도 된다.
성공 확률을 바꿔보자. 각 방문객들이 기념품 점에서 기념품을 구매할 확률이 60% 70% 90% 95%의 다른 값들로 바꿔보고, 분포 모양이 어떻게 달라지는지 확인해보자.
plt.figure(figsize = (15, 4))
plt.subplot(131)
binomial_70 = binom.pmf(k, n, p = 0.7)
# 같은 분포를 그려보자
plt.bar(k, binomial_70)
plt.title("p=%.2f" % (0.7), fontsize = 15)
plt.xlabel("Number of Successes")
plt.ylabel("Probability of Successes")
plt.subplot(132)
binomial_80 = binom.pmf(k, n , p = 0.8)
# 같은 분포를 그려보자
plt.bar(k, binomial_80)
plt.title("p=%.2f" % (0.8), fontsize = 15)
plt.xlabel("Number of Successes")
plt.ylabel("Probability of Successes")
plt.subplot(133)
binomial_90 = binom.pmf(k, n, p = 0.9)
# 같은 분포를 그려보자
plt.bar(k, binomial_90)
plt.title("p=%.2f" % (0.9), fontsize = 15)
plt.xlabel("Number of Successes")
plt.ylabel("Probability of Successes")
plt.tight_layout(w_pad = 5)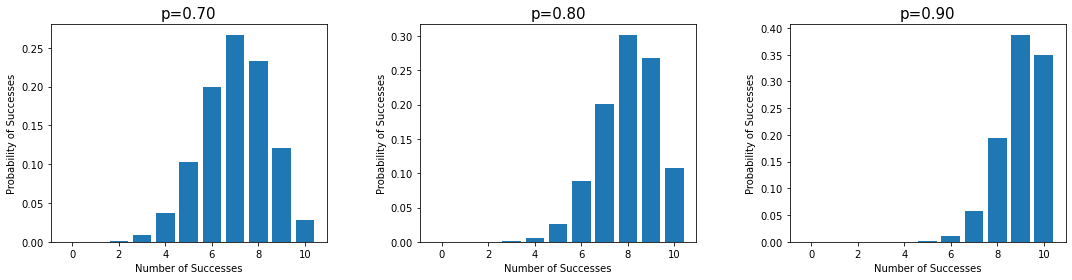
결론 :
위 그래프로 부터 p (성공할 확률)의 값이 변화할 수록 분포의 모양도 변화한다는 것이 명백해보인다.
연속 Uniform 분포
문제 설명
IT 업계는 소프트웨어 개발 초기 단계에서 소프트웨어 엔지니어가 버그를 수정해야 하는 시간을 'debugging.csv' 에 기록했습니다.
X = 버그를 고치기위해 필요한 시간 이라고 합시다.
X 는 연속형 랜덤 변수입니다. X의 분포를 살펴보고, 다음 질문에 답해봅시다.
- 임의로 선택된 소프트웨어를 디버깅하는데 소요되는 시간이 3시간보다 적을 확률을 구하세요.
- 임의로 선택된 소프트웨어를 디버깅하는데 소요되는 시간이 2시간 이상일 확률을 구하세요
- 소프트웨어 디버깅하는 시간의 50번째 퍼센타일 (=중앙값) 을 구하세요.
데이터를 데이터프레임으로 읽어봅시다.
debugging = pd.read_csv("debugging.csv")
debugging.head()
버그를 고치는데 소요되는 최소 시간과 최대 시간을 파라미터로 사용하여 uniform 분포의 PDF와 함께, 데이터의 히스토그램을 그려봅시다.
plt.hist(debugging["Time Taken to fix the bug"], density = True)
plt.axhline( 1 / 4 , color = "red")
plt.xlabel("Time required for bug fixing")
plt.ylabel("Probability")
plt.title("Data Distribution")
plt.show()
데이터의 uniform 분포를 인식하는 또다른 방식은 밀도 그림을 확인해보는 것입니다. seaborn library의 distplot을 사용하여 버그를 고치는데, 필요한 시간 분포를 시각화해 봅시다.
# 버그를 수정하는데 필요한 시간에 대한 density plot
sns.distplot(debugging["Time Taken to fix the bug"], kde = True)
plt.show()
인사이트 : 위 그림 에서 봤듯이, 모든 값들이 1과 5 에 거의 동등한 확률로 분포되어 있기에, 우리는 연속형 uniform 분포를 사용할 것이다. 우리는 끝 점을 결정할 필요가 잇다. 여기, 끝점은 1과 5이다.
X ~ U(1,5)
# 필요한 함수 import
from scipy.stats import uniform
# uniform.pdf() 를 사용해서, 확률 분포를 생성함
x = np.linspace(1, 5, 50)
probs = uniform.pdf(x, loc = 1, scale = 4)임의로 선택된 소프트웨어를 디버깅하는데 걸리는 시간이 최대 3시간 이상일 확률을 구하시요
CDF : 임의의 변수 (X) 는 x 보다 적거나 같은 값을 가질 확률이다. 아래 처럼 나타낼 수 있다. Fx(X) = P(X <= x)
P(X <= 3)
# 확률 분포를 그려보자
# 계산을 더 잘 시각화 하기 위해 여기서 분포를 그래볼 것이다.
# 물론, 위 질문에 답하기 위해 시각화를 만들 필요는 없다.
# 직접적으로 확률 값을 구하기 위한 cdf 값을 사용해도 된다.
x1 = np.linspace(1, 3, 25)
plt.plot(x, probs)
plt.fill_between(x, probs)
plt.fill_between(x1, uniform.pdf(x = x1, loc = 1, scale = 4), color = "r")
plt.xlabel("Time required for bug fixing")
plt.ylabel("Probability")
plt.title("Continuous Uniform Distribution: X ~ U(1,5)")
plt.show()
위의 그래프에서 볼 수 있듯이, 빨간색 부분이 P(X <= 3)을 나타낸다. 임의로 선택된 소프트웨어 디버깅을 하는데 소요되는 시간이 최대 3시간 이상 걸릴 확률을 구해보자. 우리는 uniform.cdf() 함수를 사용할 것이다.
uniform.cdf(x = 3, loc = 1, scale = 4)
>>> 0.5임의로 선택된 소프트웨어 버그를 수정하는데 걸리는 시간이 2시간 초과일 확률을 구해라
P(X > 2)
# 확률 분포를 그려보자
# 계산을 더 잘 시각화 하기 위해 여기서 분포를 그래볼 것이다.
# 물론, 위 질문에 답하기 위해 시각화를 만들 필요는 없다.
# 직접적으로 확률 값을 구하기 위한 cdf 값을 사용해도 된다
x1 = np.linspace(2, 5, 20)
plt.plot(x, probs)
plt.fill_between(x, probs)
plt.fill_between(x1, uniform.pdf(x = x1, loc = 1, scale = 4), color = "r")
plt.xlabel("Time required for bug fixing")
plt.ylabel("Probability")
plt.title("Continuous Uniform Distribution: X ~ U(1,5)")
plt.show()
위 그래프에서, 빨간색 부분이 P(X>2)를 나타낸다. 임의로 선택한 소프트웨어를 고치는데 걸리는 시간이 2시간 초과일 확률을 구해보자. 우리는 uniform.cdf() 함수를 사용할 것이다.
X ~ U(1,5) 라서 loc = 1 , scale = 5-1 = 4
1 - uniform.cdf(x = 2, loc = 1, scale = 4)
>>> 0.75소프트웨어 디버깅하는데 걸리는 시간의 50번째 퍼센타일을 구해보자. ppf(): 주어진 지점의 퍼센타일 포인트를 계산하는 함수이다. cdf와 반대이다.
uniform.ppf(q = 0.5, loc = 1, scale = 4)
>>> 3.0결론:
디버깅하는데 걸리는 시간이 3시간 보다 적을 가능성은 50% 정도이고, 2시간 이상 걸릴 가능성은 75% 정도이다.
디버깅 시간의 중앙값 (50번째 퍼센타일)은 3시간 이다 .
정규 분포 (Normal Distribution)
문제 설명
한 시험 기관에서는 2020 년도에 치뤄진 SAT 시험의 복잡성을 분석하기를 원한다. 그들은 1000명의 학생들의 SAT 점수를 "sat_score.csv" 파일에 수집했다. 2020년도 SAT 시험의 복잡성을 결정하도록 도와주는 다음 질문에 대답해보자.
- 한 학생이 SAT 시험에서 800점 이하의 점수를 받을 확률을 구하시오
- 한 학생이 SAT 시험에서 1300점 이상의 점수를 받을 확률을 구하시오 .
- 90번째 퍼센타일에 보장하기 위해 반드시 받아야 되는 최소 점수를 구하세요.
- 상위 5% 안에 들기위해 반드시 받아야되는 최소 점수를 구하세요.
Data를 Dataframe으로 읽어봅시다.
sat_score = pd.read_csv("sat_score.csv")
sat_score.head()
SAT 점수의 평균과 표준편차 (파라미터) 를 계산해 봅시다.
# 필요한 함수를 불러옵니다.
from scipy.stats import norm
# SAT 점수 데이터의 평균과 표준 편차를 구해봅시다.
mu = sat_score['score'].mean()
sigma = sat_score['score'].std()
print("The estimated mean is ", round(mu, 2))
print("The estimated standard deviation is", round(sigma, 2))
>>> The estimated mean is 1007.46
The estimated standard deviation is 204.43분포를 그려봅시다.
파라미터 (평균 (mu) 와 표준편차 (sigma))를 사용하는 것은, 데이터의 모양을 분석하고, 정규분포의 pdf를 시각화하는데 도움을 줄 것입니다.
# SAT 점수의 PDF를 norm.pdf() 를 사용하여 계산해봅시다.
# 빈 데이터 프레임을 만듭니다
density = pd.DataFrame()
# sat 점수의 최소값과 최댓값 범위에서 100개의 배열을 만들고, 빈 데이터 프레임의 첫번째 열에 저장합니다.
density['x'] = np.linspace(
sat_score['score'].min(), sat_score['score'].max(), 100
)
# 만들어진 점수의 pdf()를 계산하고, 'pdf' 라는 컬럼 명에 저장합니다.
density['pdf'] = norm.pdf(density['x'], mu, sigma)
# subplots 를 만듭니다.
fig, ax = plt.subplots()
# histogram을 사용하여 데이터 분포를 그립니다.
sns.histplot(sat_score["score"] , ax = ax , kde = True, stat = 'density')
# 정규 분포의 pdf를 그립니다.
ax.plot(density['x'], density['pdf'], color = 'red')
# 제목을 작성합니다.
plt.title("Normal Distribution")
# 그림을 표시합니다.
plt.plot()
인사이트 : 위 그림에서 볼 수 있듯이, 빨간색과 파란색의 두가지 곡선이 있습니다. 파란색 곡선은 데이터 분포의 모양을 나타내고, 빨간색 곡선은 PDF (Probability density function) 를 나타냅니다. 이 데이터는 정규분포에 가깝습니다. 그래서 우리는 데이터 분포가 정규분포를 따른다고 가정할 수 있고, 정규성 가정에 근거한 계산을 수행할 수 있습니다.
학생이 SAT 시험에서 800점보다 더 작은 점수를 받을 확률을 구하시오
# 누적 확률을 계산해봅시다.
# norm.cdf() 로 계산해봅시다.
prob_less_than_800 = norm.cdf(800, mu, sigma)
print(
"The probability that a student will score less than 800 is",
round(prob_less_than_800, 4)
)
>>> The probability that a student will score less than 800 is 0.1551# 확률 분포를 그려봅시다.
# 계산을 더 잘 시각화 하기 위해서 분포를 그려볼 것입니다.
# 물론, 문제에 대한 답을 하기 위해 시각화를 할 필요는 없습니다.
# 확률 계산을 위해, cdf 함수를 직접적으로 사용할 수 있습니다.
# 정규 분포의 pdf를 그려봅시다.
plt.plot(density["x"], density["pdf"])
# x = 800 인 곳에 빨간색 수직선을 그려봅시다.
plt.axvline(x = 800, c = "r")
# SAT 점수의 최솟값과 800 사이의 50개의 배열을 만들어봅시다.
x1 = np.linspace(density["x"].min(), 800, 50)
# 정해진 영역에 빨간색으로 채웁시다.
plt.fill_between(x1, norm.pdf(x1, mu, sigma), color = 'r')
# x-axis 의 라벨을 작성합시다.
plt.xlabel("Score")
# y-axis 의 라벨을 작성합시다.
plt.ylabel("Probability")
# 제목을 작성합시다.
plt.title("Normal Distribution")
# plot을 그려봅시다.
plt.show()
학생이 SAT 시험에서 1300점 이상 받을 확률을 구하시오
# 누적 확률을 구하고, 1300점 이상 받을 누적 확률을 제거합시다.
prob_greater_than_1300 = 1 - norm.cdf(1300, mu, sigma)
print(
"The probability that a student will score more than 1300 is",
round(prob_greater_than_1300, 4),
)
>>> The probability that a student will score more than 1300 is 0.0762# 확률 분포를 그리자
# 계산을 더 잘 시각화 하기 위해서 분포를 그려볼 것입니다.
# 물론, 문제에 대한 답을 하기 위해 시각화를 할 필요는 없습니다.
# 확률 계산을 위해, cdf 함수를 직접적으로 사용할 수 있습니다.
plt.plot(density["x"], density["pdf"])
plt.axvline(x = 1300, c = "r")
x1 = np.linspace(1300, density["x"].max(), 50)
plt.fill_between(x1, norm.pdf(x1, mu, sigma), color = 'r')
plt.xlabel("Score")
plt.ylabel("Probability")
plt.title("Normal Distribution")
plt.show()
학생이 90번째 percentile에 들어갈 최소 점수를 구하시오
# 90번째 퍼센타일 점수를 ppf() 함수로 구해볼 것이다.
# norm.ppf()는 퍼센타일 지점을 구해볼 것이다.
score_90th_percentile = norm.ppf(0.90, mu, sigma)
print(
"The 90th percentile score should be", round(score_90th_percentile)
)
>>> The 90th percentile score should be 1269# 확률 분포를 그려봅시다.
# 계산을 더 잘 시각화 하기 위해서 분포를 그려볼 것입니다.
# 물론, 문제에 대한 답을 하기 위해 시각화를 할 필요는 없습니다.
# 확률 계산을 위해, cdf 함수를 직접적으로 사용할 수 있습니다.
plt.plot(density["x"], density["pdf"])
plt.axvline(x = score_90th_percentile, c = 'r')
plt.xlabel("Score")
plt.ylabel("Probability")
plt.title("Normal Distribution")
plt.show()
상위 5% 안에 들기위한 최소 점수를 구해봅시다.
# 95번째 퍼센타일 점수를 ppf() 함수로 구해봅시다.
score_top_five_percent = norm.ppf(0.95, mu, sigma)
print("The minimum score to be in top 5% should be",
round(score_top_five_percent)
)
>>> The minimum score to be in top 5% should be 1344# 확률 분포를 그려봅시다.
# 계산을 더 잘 시각화 하기 위해서 분포를 그려볼 것입니다.
# 물론, 문제에 대한 답을 하기 위해 시각화를 할 필요는 없습니다.
# 확률 계산을 위해, cdf 함수를 직접적으로 사용할 수 있습니다.
plt.plot(density["x"], density["pdf"])
plt.axvline(x = score_top_five_percent, c = 'r')
plt.xlabel("Score")
plt.ylabel("Probability")
plt.title("Normal Distribution")
plt.show()
결론 :
1) 오직 학생의 15.51% 만 800점 이하의 점수를 얻었고, 학생의 7.62% 가 1300점 이상 점수를 얻었다. 이를 통해 2020년의 SAT 점수가 평이한 것으로 보인다.
2) 학생이 90번째 퍼센타일 안에 들려면 최소 1269점을 받아야한다.
3) 학생이 상위 5% 안에 들려면 최소 1344점을 받아야한다.
정규 변수의 표준화
SAT 점수는 평균 1000과 표준편차 200의 정규분포이고, ACT 점수는 평균 20과 표준편차 5의 정규분포라고 가정했다고 하자.
한 대학은 입학처에 SAT점수와 ACT 점수만 제공한다. 대학 입학처는 교수진들을 위해 모든 지원자들 간에서 가장 잘 수행한 상위 학생들을 결정해야한다. 지원자들 중 SAT에서 가장 높은 점수를 받은 사람은 1350점이고, ACT에서 가장 높은 점수를 받은사람은 30점 이라고 하자.
교수진들을 위해 최고의 후보진들을 선택해보자 !
# SAT와 ACT 점수의 두 분포를 그려봅시다.
from scipy.stats import norm
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (12,4) )
x = np.linspace(400, 1600, 1000)
ax1.plot(x, norm.pdf(x, loc = 1000, scale = 200), color = 'b')
ax1.set_title("Normal Distribution of SAT scores")
ax1.set_xlabel("SAT scores")
ax1.set_ylabel("Probability")
ax1.axvline(1350, ymax = 0.23, linestyle = '--', color = 'green')
x1 = np.linspace(1, 36, 100)
ax2.plot(x1, norm.pdf(x1, loc = 20, scale = 5), color = 'r')
ax2.set_title("Normal Distribution of ACT scores")
ax2.set_xlabel("ACT scores")
ax2.set_ylabel("Probability")
ax2.axvline(30, ymax = 0.18, linestyle = '--', color = 'green')
plt.show()
위 그림에서 볼 수 있듯, 파란색 곡선은 SAT 점수 분포를 나타내고, 빨간색 곡선은 ACT 점수 분포를 나타낸다. SAT와 ACT 시험에서 지원자들의 가장 높은 점수는 각각의 분포에 녹색점선으로 표시했다. 그러나, 우리가 가장 높은 점수의 원래 점수를 비교하기에는 어렵다. 그래서, 두 점수를 표준화 하여 Z-scores를 비교할 필요가 있다.
# SAT에서 지원자들 간의 가장 높은 점수의 Z-score 를 구하시오
top_sat = (1350 - 1000) / 200
print("The Z-score of highest scorer in SAT among all the applicatns", top_sat)
# ACT에서 지원자들 간의 가장 높은 점수의 Z-score 를 구하시오
top_act = (30 - 20) / 5
print("The Z-score of highest scorer in ACT among all the applicatns", top_act)
>>> The Z-score of highest scorer in SAT among all the applicatns 1.75
The Z-score of highest scorer in ACT among all the applicatns 2.0표준 정규 분포를 그리고 위 표준 점수를 시각화 해보자
# 표준 정규 분포를 그리고
# 표준 점수를 시각화 하고
# 계산을 더 잘 시각화 하기위해 분포를 그려보자.
fig, ax = plt.subplots()
x = np.linspace( -4, 4, 50)
ax.plot(x, norm.pdf(x, loc = 0, scale = 1), color = 'b')
ax.set_title('Standard Normal Distribution')
ax.set_xlabel('Z-scores')
ax.set_ylabel('Probability')
ax.axvline(top_sat, ymax = 0.25, linestyle = '--', color = 'green')
ax.axvline(top_act, ymax = 0.16, linestyle = '--', color = 'black')
plt.show()
위 그래프에서, 초록색 선은 지원자들의 표준화된 가장 높은 SAT 점수가 평균보다 표준편차의 1.75배 더 위에 있음을 의미하고, 검정색 선은 지원자들의 표준화된 가장 높은 ACt 점수가 평균보다 표준편차의 2배 더 위에 있음을 의미한다.
이것은 지원자들 사이에서 ACT 에서 가장 높은 점수를 받은 사람이 SAT에서 가장 높은 점수를 받은 사람보다 더 잘 했다는 것을 의미한다.
그래서 교수진들은 ACT 점수에서 가장 높은 점수를 받은 사람들을 고려해야한다.
중심극한정리 (CLT)
중심극한 정리는 우리가 모집단에서 다수의 샘플을 독립적으로 추출했을 때, 각 샘플의 평균을 계산해보고, 이것들을 그려본다면 (표본 평균들), 그려진 그림은 모집단의 분포와는 상관 없이, 표본의 크기가 증가함에 따라, 정규 분포를 띄는 경향이 있다는 것을 의미합니다.
python 시뮬레이션을 사용해서 CLT를 확인해 봅시다.
여기 Uniform 분포가 있습니다. ( Normal이 아닌 것으로 가장 많이 정의됩니다. )
# 필요한 함수를 불러옵시다.
from scipy.stats import uniform
# 재현성을 위해 seed를 세팅합시다
np.random.seed(1)
# 크기가 100,000인 uniform분포를 생성합시다.
uniform_pop = uniform.rvs(0, 10, size = 100000)
# uniform 분포를 시각화해봅시다.
plt.hist(uniform_pop)
plt.title("Uniform Distribution Population")
plt.xlabel("X ~ U(0, 10)")
plt.ylabel("Count")
plt.show()
이 분포에서 표본 분포를 만들어봅시다. (sample size = 5, number of samples = 500)
- size 가 5인 샘플을 추출해봅시다. 즉 n = 5 이고, 우리는 5개의 독립 관찰 표본을 추출해볼 것입니다.
- 각 5개의 관찰 값들의 평균을 구해봅시다. 즉 - 표본 평균입니다.
- 위의 2단계를 500번 반복해봅시다. 그래서 n = 5 인 500개의 표본 평균을 구해봅시다.
# 재현성을 위해 seed를 세팅합니다.
np.random.seed(1)
# 표본의 크기를 5로 설정합니다.
n = 5
# 샘플 평균을 저장할 리스트 입니다.
sample_means = []
# 다수의 샘플을 추출할 루프를 반복합니다.
for j in range(500):
# size 가 n 인 표본을 추출합니다.
sample = np.random.choice(uniform_pop, size = 5)
# 표본 평균을 계산합니다.
sample_mean = np.mean(sample)
# 표본 평균을 리스트에 추가합니다.
sample_means.append(sample_mean)
# 표본 평균의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("sample mean")
plt.ylabel("Count")
plt.show()
sample size를 15로 증가시켜 (n = 15) 또 다른 샘플링 분포를 만들어 봅시다.
# 재현성을 위해 seed를 세팅합니다.
np.random.seed(1)
# 표본의 크기를 5로 설정합니다.
n = 15
# 샘플 평균을 저장할 리스트 입니다.
sample_means = []
# 다수의 샘플을 추출할 루프를 반복합니다.
for j in range(500):
# size 가 n 인 표본을 추출합니다.
sample = np.random.choice(uniform_pop, size = n)
# 표본 평균을 계산합니다.
sample_mean = np.mean(sample)
# 표본 평균을 리스트에 추가합니다.
sample_means.append(sample_mean)
# 표본 평균의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("sample mean")
plt.ylabel("Count")
plt.show()
sample size를 30으로 증가시켜 봅시다.
# 재현성을 위해 seed를 세팅합니다.
np.random.seed(1)
# 표본의 크기를 5로 설정합니다.
n = 30
# 샘플 평균을 저장할 리스트 입니다.
sample_means = []
# 다수의 샘플을 추출할 루프를 반복합니다.
for j in range(500):
# size 가 n 인 표본을 추출합니다.
sample = np.random.choice(uniform_pop, size = n)
# 표본 평균을 계산합니다.
sample_mean = np.mean(sample)
# 표본 평균을 리스트에 추가합니다.
sample_means.append(sample_mean)
# 표본 평균의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("sample mean")
plt.ylabel("Count")
plt.show()
sample size를 50으로 증가시켜 봅시다.
# 재현성을 위해 seed를 세팅합니다.
np.random.seed(1)
# 표본의 크기를 5로 설정합니다.
n = 50
# 샘플 평균을 저장할 리스트 입니다.
sample_means = []
# 다수의 샘플을 추출할 루프를 반복합니다.
for j in range(500):
# size 가 n 인 표본을 추출합니다.
sample = np.random.choice(uniform_pop, size = n)
# 표본 평균을 계산합니다.
sample_mean = np.mean(sample)
# 표본 평균을 리스트에 추가합니다.
sample_means.append(sample_mean)
# 표본 평균의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("sample mean")
plt.ylabel("Count")
plt.show()
Insigt
- sampe size가 증가함에 따라 샘플링 분포는 정규분포에 가까워진다는 것을 확인해볼 수 있었다.
모집단 분포가 정규분포일 때를 확인해보자
# 필요한 함수를 불러옵시다.
from scipy.stats import norm
# 재현성을 위해 seed를 세팅합시다.
np.random.seed(1)
# size가 100000인 정규분포 모집단을 만듭시다.
normal_pop = norm.rvs(0, 1, size = 100000)
# 정규 분포를 시각화해 봅시다.
plt.hist(normal_pop , 200)
plt.title("Normal Distribution Population")
plt.xlabel("X~N(0,1)")
plt.ylabel("Count")
plt.show()
이 분포에서 표본 분포를 만들어봅시다. (sample size = 5, number of samples = 500)
- size 가 5인 샘플을 추출해봅시다. 즉 n = 5 이고, 우리는 5개의 독립 관찰 표본을 추출해볼 것입니다.
- 각 5개의 관찰 값들의 평균을 구해봅시다. 즉 - 표본 평균입니다.
- 위의 2단계를 500번 반복해봅시다. 그래서 n = 5 인 500개의 표본 평균을 구해봅시다.
이제 표본 분포의 모양을 관찰해볼 것입니다.
# 재현성을 위해 seed를 세팅합니다.
np.random.seed(1)
# size = 5 로 세팅합니다.
n = 5
# 표본 평균을 저장할 리스트 입니다.
sample_means = []
# 다수 샘풀을 추출하기 위해 루프를 반복합니다.
for j in range(500):
# size 가 n 인 샘플을 추출합니다.
sample = np.random.choice(normal_pop, size = n)
# 표본 평균을 계산합니다.
sample_mean = np.mean(sample)
# 리스트에 추가합니다.
sample_means.append(sample_mean)
# 표본 평균들의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("Sample mean")
plt.ylabel("Count")
plt.show()
Insigt
- 모집단 분포가 정규분포일때, 표본 분포는 표본 크기가 n = 5 처럼 작을 때에도 정규 분포에 거의 근사합니다.
표본의 크기가 n = 15 일때도, 확인해봅시다.
# 재현성을 위해 seed를 세팅합니다.
np.random.seed(1)
# size = 5 로 세팅합니다.
n = 15
# 표본 평균을 저장할 리스트 입니다.
sample_means = []
# 다수 샘풀을 추출하기 위해 루프를 반복합니다.
for j in range(500):
# size 가 n 인 샘플을 추출합니다.
sample = np.random.choice(normal_pop, size = n)
# 표본 평균을 계산합니다.
sample_mean = np.mean(sample)
# 리스트에 추가합니다.
sample_means.append(sample_mean)
# 표본 평균들의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("Sample mean")
plt.ylabel("Count")
plt.show()
표본의 크기가 n = 30 일때도, 확인해봅시다.
# 재현성을 위해 seed를 세팅합니다.
np.random.seed(1)
# size = 5 로 세팅합니다.
n = 30
# 표본 평균을 저장할 리스트 입니다.
sample_means = []
# 다수 샘풀을 추출하기 위해 루프를 반복합니다.
for j in range(500):
# size 가 n 인 샘플을 추출합니다.
sample = np.random.choice(normal_pop, size = n)
# 표본 평균을 계산합니다.
sample_mean = np.mean(sample)
# 리스트에 추가합니다.
sample_means.append(sample_mean)
# 표본 평균들의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("Sample mean")
plt.ylabel("Count")
plt.show()
CLT (중심극한정리)가 지수 분포 (Exponential Distribution) (명백하게 정규분포가 아닌 경우)에도 잘 작동하는지 확인해봅시다.
# 필요한 함수를 불러옵니다.
from scipy.stats import expon
# 재현성을 위해 seed를 고정시킵니다.
np.random.seed(1)
# 크기가 100000 인 지수 분포 모집단을 생성합니다.
exp_pop = expon.rvs(size = 100000)
# 지수 분포를 시각화해봅시다.
plt.hist(exp_pop, 200)
plt.title("Exponential Distribution Population")
plt.xlabel("X~Exp(1)")
plt.ylabel("Count")
plt.show()
Sample Size n = 5 일때 샘플링 분포를 확인해 봅시다.
# 재현성을 위해 seed를 고정시킵시다.
np.random.seed(1)
# 표본 크기를 5로 고정 시킵시다.
n = 5
# 표본 평균을 담을 리스트입니다.
sample_means = []
# 다수의 표본을 추출하기위해 루프를 반복합시다.
for j in range(500):
# size가 n인 표본을 추출합시다.
sample = np.random.choice(exp_pop, size = n)
# 표본 평균을 계산합시다.
sample_mean = np.mean(sample)
# 표본 평균을 리스트에 저장합니다.
sample_means.append(sample_mean)
# 표본 평균의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("sample mean")
plt.ylabel("count")
plt.show()
샘플 크기 n = 15 일 때, 표본 분포를 확인해봅시다.
# 재현성을 위해 seed를 고정시킵시다.
np.random.seed(1)
# 표본 크기를 5로 고정 시킵시다.
n = 15
# 표본 평균을 담을 리스트입니다.
sample_means = []
# 다수의 표본을 추출하기위해 루프를 반복합시다.
for j in range(500):
# size가 n인 표본을 추출합시다.
sample = np.random.choice(exp_pop, size = n)
# 표본 평균을 계산합시다.
sample_mean = np.mean(sample)
# 표본 평균을 리스트에 저장합니다.
sample_means.append(sample_mean)
# 표본 평균의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("sample mean")
plt.ylabel("count")
plt.show()
샘플 크기 n = 30 일 때, 표본 분포를 확인해봅시다.
# 재현성을 위해 seed를 고정시킵시다.
np.random.seed(1)
# 표본 크기를 5로 고정 시킵시다.
n = 30
# 표본 평균을 담을 리스트입니다.
sample_means = []
# 다수의 표본을 추출하기위해 루프를 반복합시다.
for j in range(500):
# size가 n인 표본을 추출합시다.
sample = np.random.choice(exp_pop, size = n)
# 표본 평균을 계산합시다.
sample_mean = np.mean(sample)
# 표본 평균을 리스트에 저장합니다.
sample_means.append(sample_mean)
# 표본 평균의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("sample mean")
plt.ylabel("count")
plt.show()
샘플 크기 n = 50 일 때, 표본 분포를 확인해봅시다.
# 재현성을 위해 seed를 고정시킵시다.
np.random.seed(1)
# 표본 크기를 5로 고정 시킵시다.
n = 50
# 표본 평균을 담을 리스트입니다.
sample_means = []
# 다수의 표본을 추출하기위해 루프를 반복합시다.
for j in range(500):
# size가 n인 표본을 추출합시다.
sample = np.random.choice(exp_pop, size = n)
# 표본 평균을 계산합시다.
sample_mean = np.mean(sample)
# 표본 평균을 리스트에 저장합니다.
sample_means.append(sample_mean)
# 표본 평균의 히스토그램을 그려봅니다.
sns.distplot(sample_means, kde = True)
plt.title("Distribution of Sample Means for n = " + str(n))
plt.xlabel("sample mean")
plt.ylabel("count")
plt.show()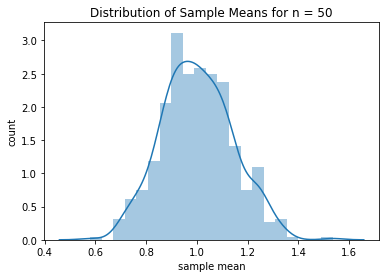
Key Takeaway (결론)
- 3가지 다른 분포로부터 CLT의 근본 아이디어를 시뮬레이션 해보있다. 모집단 분포의 모양이 어떻든, 표본 평균 분포는 샘플 사이즈가 증가할 수록 정규분포에 근사한다는 사실을 알 수 있다.
점 추정 (Point Estimation)
어떻게 모집단 평균이 표본 평균으로 추정되는지 확인해봅시다.
한 비영리 단체가 지역 산림 부서의 파일을 샘플로 추출하여, 10건의 산불 사고에 대해 다음과 같은 금액 (수천 달러)의 피해액을 산출했습니다.
120, 55, 60, 10, 8, 150, 44, 58, 62, 123
이 지역의 산불로 인한 피해액의 평균 추정치는 얼마 인가요?
# sample data를 가져옵시다.
sample = np.array([120, 55, 60, 10, 8, 150, 44, 58, 62, 123])
# sample 의 평균을 계산합시다.
x_bar = np.mean(sample)
x_bar
>>> 69.0insigt
- 이 지역의 산불 화재의 피해액의 평균 추정치는 $69000. 입니다.
일반적으로 알 수 없는 모집단 모수의 점 추정치는 해당 표본 통계랑 입니다.
예를 들어보면 :
a. 모집단 평균 μ는 표본 평균 𝑋¯X¯ 에 의해 추정됩니다.
b. 모집단 중앙값 은 표본 중앙값 𝑋̃ X~ 에 의해 추정됩니다.
c. 모집단의 성공 비율 π 는 표본의 성공 비율 p 에 의해 추정됩니다.
신뢰 구간
어떻게 표준 편차 (std) 가 알려져 있을 때, 모집단 평균을 추정하기위핸 신뢰 구간을 어떻게 찾는지 확인해봅시다.
모집단의 평균이 아닌 표준 편차를 아는 경우는 거의 없다. 하지만, 생각보다 가능성이 낮은 가정은 아닐 수도 있다. 장시간 사용되는 타이트한 제조공정의 경우, 공정의 변동성을 제어할 수 있지만, 온도나 습도의 작은 변화로 평균은 변동될 수 있습니다.
모집단 평균은 알 수 없고, 표준 편차를 알고 있는 예제애 대해서 신뢰 구간을 구성해보겠습니다.
새 커피 머신에서 제공한 블랙 커피 50잔의 랜덤 표본에 대해서 카페인 함량(mg)이 조사되었습니다. 샘플의 평균은 110mg이 되는 것으로 밝혀졌습니다. 제조사의 모든 기계로 부터의 표준 편차는 7mg으로 알려져있습니다. 기계에 의해 분배된 컵의 평균 카페인 함량인, 모집단 평균 μ에 대한 신뢰도 95%의 신뢰구간을 구성해봅시다.
# 필요한 함수를 불러옵시다.
from scipy.stats import norm
# 표본 평균과 표준 편차 (sigma) 값을 세팅합시다.
x_bar, sigma = 110, 7
# 표본 크기 값을 세팅합시다
n = 50
# 신뢰 구간을 구성합시다.
np.round(norm.interval(0.95, loc = x_bar, scale = sigma / np.sqrt(n)) , 2)
>> array([108.06, 111.94])Insigt
- 95%의 경우 기계가 분사하는 커피잔의 평균 카페인 함량은 108.06mg과 111.94mg 사이일 것이다.
표준편차가 알려져있지 않을때, 모집단 평균의 신뢰구간을 어떻게 찾는지 확인해봅시다.
위에서 논의되었던 예시는, 모집단의 표준 편차가 알려져있다는 가정이었습니다. 하지만 다수의 케이스에서, 이 가정은 성립되지 않습니다.
모집단의 표준 편차를 모르는 경우에는, 표준으로 부터 추정될 수 있습니다. 이 경우에서는 표본 평균이 (n-1) 자유도를 가지는 Student's t 분포를 따른다고 할 수 있습니다.
정규분포외는 달리, t-분포는 통계학 추론에서 매우 유용합니다. 이 분포는 0 을 중심으로 한 대칭 분포이기 때문이빈다. 매우 큰 자유도 에서는 t 분포가 표준 정규 분포와 거의 동일합니다. t 분포의 파라미터는 자유도 라고 알려져 있습니다.
아래에 다양한 자유도 (k) 에서의 t-분포의 그래프가 있습니다. 우리는 k 값을 증가 시키면서 정규분포와 가까워 지는지 확인해볼 수 있습니다.
# 필요한 함수를 불러옵니다.
from scipy.stats import t
from scipy.stats import norm
# x 값을 세팅합니다.
x = np.linspace(-3, 3, 100)
# 각기 다른 k 값에 대한 t 분포를 그립니다.
fig, axes = plt.subplots(2,3 , sharex = False, sharey = False, figsize = (15,10))
axes = axes.ravel() # array() 값을 리턴하지 않음
for i, k in zip(range(6), [1, 2, 3, 5, 10, 30]):
ax = axes[i]
ax.plot(x, t.pdf(x, df = k), color = "blue", label = "t dist")
ax.plot(x, norm.pdf(x), color = "red", label ="normal dist")
ax.set_title("t-distribution for k = {0}".format(k))
ax.legend(loc = "upper right", fontsize = 10)
plt.tight_layout()
모집단의 표준 편차가 알려져 있지 않을 때, t-분포를 이용해서, 평균의 신뢰 구간을 구성해봅시다.
카페인 함량 (mg)은 새로운 기계에 의해 분배된 50잔의 블랙 커피의 무작위 샘플에 대해 조사되었습니다. 샘플의 평균은 110mg 으로 조사되었고, 샘플의 표준 편차는 7mg으로 조사되었습니다. 기계에 의해 추출된 평균 카페인 함량인, μ의 95% 신뢰구간을 구성하시오.
# 필요한 함수를 불러옵니다.
from scipy.stats import t
# 표본 평균과 표본 표준 편차 값을 세팅 합니다.
x_bar , s = 110, 7
# 표본의 크기 값과 자유도를 세팅 합니다.
n = 50
k = n - 1
# 신뢰구간을 구성합니다.
np.round(t.interval(0.95, df = k, loc = x_bar, scale = s / np.sqrt(n)), 2)
>> array([108.01, 111.99])insigt
- 95% 의 경우, 머신에서 추출된 커피의 카페인 함량의 평균은 108.01 mg 과 111.99 mg 사이일 것이다.
Key Takeaways
- 모집단 평균의 신뢰구간은 모집단의 표준 편차를 알 때와 알지 못하는 두 경우 모두 구할 수 있다. 적절한 자유도를 활용한 t-분포 적용을 필요로 하는 후자의 경우가 좀 더 일반적이다.
- 신뢰 구간을 구성하는 일반적인 접근 방식은 적절한 표본 통계량을 사용하여, 모집단 모수를 추정하고, 표본 분포의 적절한 백분위 수 점을 사용하는 것입니다.
'노트 > Data Science : 데이터과학' 카테고리의 다른 글
| [Foundation of Data Science] 가설 검정 프레임워크 (0) | 2024.04.09 |
|---|---|
| [Naver Deview 2021] ClickHouse (클릭하우스) 리뷰 (1) | 2024.03.26 |
| [Foundation of Data Science] 가설 검정 (0) | 2023.11.05 |
| [Foundations of Data Science] 유산소 운동 피트니스 분석 (기술통계 분석 EDA) (0) | 2022.11.06 |
| [Foundations of Data Science] 자살률 분석 (이변량 분석 EDA) (1) | 2022.09.15 |