2024. 7. 2. 22:28ㆍ노트/Data Science : 데이터과학
https://towardsdatascience.com/a-b-testing-like-a-pro-master-the-art-of-statistical-test-selection-603eb5803586
A/B Testing Like a Pro: Master the Art of Statistical Test Selection
Real-world data can be tricky! Guide to choosing and applying the Right Statistical Test (using Python)
towardsdatascience.com
https://www.kaggle.com/code/tammyrotem/ab-tests-with-python/notebook
AB_Tests_with_Python
Explore and run machine learning code with Kaggle Notebooks | Using data from multiple data sources
www.kaggle.com
현실 데이터는 까다로울수 있습니다. python 을 사용해서 적절한 통계적 검정 기법을 선택하고 적용하는 법을 가이드하겠습니다.
A/B 테스트는 강력한 도구입니다. 하지만 잘못된 통계적 검정법을 선택하는 것은 잘못된 결과를 초래할 수 있습니다. 이 가이드는 당신의 데이터에 완벽한 데이터를 선택할수 있도록 가이드하여, 신뢰할 수 있는 분석을 보증하고, 신뢰있는 제안을 만들 수 있도록 하겠습니다.
당신의 A/B 테스트 결과를 단지 요약만 하고 싶나요? 흥미로운 점은 여기서 멈추지 않습니다. 진정한 마법은 데이터 속으로 뛰어들어 가치 있는 통찰력을 발견할 때 발생합니다. 이 가이드는 데이터 분석가 또는 데이터 사이언티스트가 A/B 테스트 결과를 분석하는 체계적인 접근 방식을 제공합니다.
분석의 큰 부분은 데이터와 데이터에 적합한 테스트를 선택하는 데 있어 복잡한 통계적 기반을 이해하는 것입니다. 이 단계는 바로 구현에 뛰어들고 중요한 통찰력을 놓칠 수 있기 때문에 종종 간과됩니다.
분석하는 내용에 따라 다양한 가정을 설정할 수 있으며 따라서 선택할 수 있는 테스트 세트도 다릅니다. 이 문서에서는 데이터에 대한 '올바른' 테스트를 선택하는 방법을 안내합니다.
가이드
바로 시작해봅시다. 이 표는 A/B 테스트의 일반적인 목표가 초점을 맞출 수 있는 일반적인 모바일 앱의 측정 지표에 초점을 맞추고 있지만, 원칙과 가정은 전체에 적용됩니다.
| 지표 종류 (Metric Type) | 추천하는 통계적 검정 기법 | 가정 | 사용해야할 때 |
| 사용자 지표 당 평균 (Average per User Metrics) |
Welch's t-test | 1. 정규 분포 2. i.i.d 3. Uneqaul variances |
- 상당히 대칭적인 데이터 (>10000) - 두 코호트의 분산이 다를때 |
| Student's t-test | 1. 정규 분포 2. i.i.d 3. Equal variances |
- 상당히 대칭적인 데이터 (>10000) - 두 코호트의 분산이 다르지 않을 때 |
|
| Mann-Whitney U-test | 1. 특별한 통계적 분포가 아님, 2. 두 그룹이 같은 분포 모양을 가짐 |
- 아웃라이어가 존재할때 - 정규성이 염려될때 - 작은 표본일 때 - 비대칭 분포일때 |
|
| 범주형 지표 (Categorical Metrics) |
Two proportion z-test | 1. 이항분포 2. i.i.d |
- Binomial Data ex. 유지했는지/이탈했는지 ex. 소비했는지/소비하지않았는지 |
| Chi-Squared Test | 1. 다수의 그룹 2. 독립적 |
- Discrete Data ex. 범주형 갯수, 사용자들의 액션 |
|
| ANOVA | 1. 다수의 그룹 2. 정규 분포 3. i.i.d 3. Equal variances |
- Continuous Variables ex. 유저당 평균, 반응 시간 |
|
| 결합 지표 (Joint Metrics) |
Delta t-test | 1.정규분포가 아닐때, 2. 독립이 아닐때 |
결합 분포로 형성되는 2개의 랜덤 변수의 비율 ex) # of clicks / # of Views ex. 클릭률, 페이지뷰당 설치수 |
어떻게 적합한 검정 방법을 결정하고, 파이썬으로 계산하는지 아래의 각 지표 유형들에 대하여 설명하는 필요한 부분들로 넘어가세요.
Section 1 : 사용자 지표 당 평균 Average per User Metrics
Section 2 : 범주형 지표 Categorical Metrics
Section 3 : 결합 지표 Joint Metrics
시작하기 전에, 기초적인 정의에 대한 설명을 하겠습니다. :
귀무가설 (Null Hypothesis):
각 가설 검정은 검정하기 위한 "이론"으로 구성되며, 이를 귀무가설(H0)이라고 한다. 우리의 분석의 목표는 이 가설이 사실인지 아닌지를 자신 있게 증명하는 것이다.
귀무가설(H ₀)은 두 집단 간에 차이가 없다고 가정하는데, 즉 feature 가 영향을 주지 않는다는 것이다.
E.g. H0:μ1=μ2
Ha:μ1≠μ2
신뢰수준 (Significance Level (Alpha)):
유의 수준, 즉 알파(α)는 검정 결과가 통계적으로 유의한지 아닌지를 결정하는 척도이다. 이는 검정을 실행하기 전에 기본 가정의 일부를 형성한다.
간단히 말해서, 유의 수준은 여러분이 발견한 것이 단순히 운이 아니라 신뢰할 수 있는지를 판단하는 데 도움이 됩니다. "야, 이건 단순한 우연이 아니라 아마도 진짜일 거야."라고 말하는 임계점 역할을 합니다
P-Value :
p-값, 즉 확률값은 귀무 가설에 대한 증거의 강도를 결정하는 데 도움이 되는 통계학에서 사용되는 척도입니다.
간단히 말하면 p-값은 거짓 양성(false positive) 결과를 얻을 확률, 즉 우리가 얻은 데이터가 우연에 의한 것이고 우리는 유형 I 오류를 범한다.
p-값이 높으면 거짓 양성(false positive) 결과에 착지할 가능성이 높아 데이터를 신뢰할 수 없다. 데이터를 신뢰할 수 없다면(즉, p-값이 높으면) H ₀을 자신 있게 증명하거나 반증할 수 없다.
P-value < 유의 수준 → H0을 기각합니다. 두 그룹이 유의하게 다르다는 결론을 내릴 수 있는 충분한 데이터가 있습니다.
P-value > 유의 수준 → H0을 기각하지 마십시오. 두 그룹이 유의하게 다르다는 결론을 내릴 수 있는 충분한 데이터가 없습니다.
분석할 지표를 선택하기:
시작하기 전에, A/B 테스트로 부터 분석하고자할 것을 이해하는 것은 중요합니다.
예를들어, 유저의 첫번째 경험을 개선하고자 한다면 (FTUE) ? 유저 리텐션이나 전환율과 같은 지표에 관심있을 것입니다. 이것은 전형적인 yes/no (1 or 0) 결과를 포함하여, "Two Proportion Z Test" 가 적합할 것입니다.
위 가이드에서 언급한 다양한 유형의 메트릭을 살펴보고, 메트릭을 선택할 수 있는 이유와 데이터가 테스트 요구 사항과 일치하는지 확인하는 방법을 설명합니다.
데이터 세팅하기:
나는 당신이 Unique ID, Variant, Metric 컬럼으로 구성되어있는 데이터를 이미가지고 있다고 가정하겠습니다.
#Separate the data into 2
group_A = df[df['Variant'] == "A"]["Metric"]
group_B = df[df['Variant'] == "B"]["Metric"]
#Change "A" and "B" to the relevant groups in your dataset
#Change "Metric" to the relevant column name with the values
Section 1 : 사용자 지표 당 평균 Average per User Metrics
이유형은 분석할 가장 흔한 지표 유형입니다. 데이터 표본이 서로 독립적이라는 것을 가정합니다.
실제 많은 케이스들의 경우, ARPU (유저당 평균 수익) 또는 유저당 평균 소비 시간과 같은 유저 지표의 평균값들은 매우 분석이 흔합니다. 만약 샘플사이즈가 충분히 크다면, 뒤로 넘어가서 Welch's t-test를 사용하면 됩니다.

이제 각 흐름을 살펴보고 사용할 경로를 결정하는 단계를 설명하겠습니다 -
Flow 1: 큰 표본 또는 정규 분포
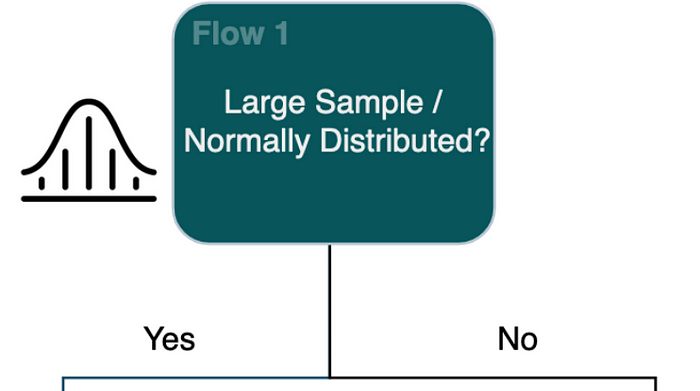
일반적으로 '대규모 표본'에 대한 나의 일반적인 가정은 개별 표본의 수가 10,000개 이상인 경우이지만, 이 정의는 상대적이며 특정 연구 분야, 수행 중인 분석 유형, 감지해야 하는 효과 크기 등 다양한 요인에 따라 다를 수 있다.
만약 n이 상대적으로 작다면, T-test를 선택해야하는지 결정하기 위해 정규성 검증을 수행하세요. 정규성 검증을 하는데 몇가지 방법이 있습니다. 확인하는 가장 쉬운 방법은 히스토그램을 생성하고, 데이터를 시각적으로 조사해보는 방법입니다. 만약 약간 정규 분포처럼 보인다면, 계속하세요. 만약 여전히 확실하지 않다면, 정규성 검정을 위해 좀 더 Shapiro-Wilkes test와 같은 통계적인 검증을 수행하는 것이 좋습니다. 여기 정규성 검정하는 다양한 기법들에 대한 좋은 아티클이 있습니다. 각각의 통계적 검정은 보통 데이터에 대해 다양한 가정을 한다는 것을 명심해야 하므로, 정규성 적합 검정을 선택하기 전에 이 점을 염두에 두어야 합니다.
히스토그램을 만들거나 Shapiro-Wilkes 검정이라는 통계 검정을 사용하여 육안 검사를 통해 데이터의 정규성을 검정하는 방법을 보여주는 아래 코드 스니펫을 참조하십시오.
Test for Normality
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
alpha=0.05 #We assume an alpha here of 0.05
# Creating Histograms
grouped = df.groupby('Variant')
#Variant column identifies the group of the user - group_A / group_B etc
# Plotting histograms for each group to visually inspect the shape of the data
for name, group in grouped:
plt.hist(group['Metric'])
plt.title(name)
plt.show()
# Shapiro-Wilkes Test to statistically test for normality
for name, group in grouped:
shapiro_test = stats.shapiro(group['Value'])
print(f"Shapiro-Wilk Test for Group {name}: W = {shapiro_test[0]}, p-value = {shapiro_test[1]}")
if p_value < alpha:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
Flow 2: 등분산?
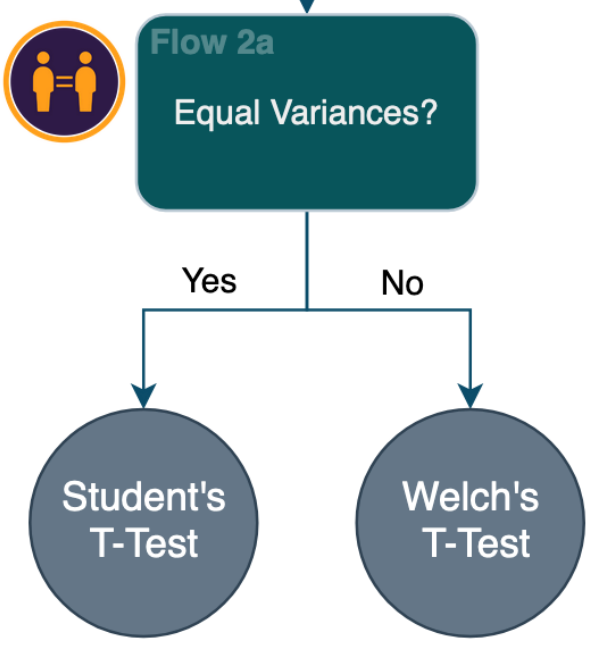
위의 Average Per User(사용자당 평균) Flowchart에서 이어집니다 -
만약 당신의 데이터가 정규성을 만족한다고 확인했다면, 다음 단계는 데이터셋이 동일한 분산을 가지는지 확인하는 단계입니다. 이것은 Welch's t-test 인지 Student's t-test 인지 결정하는 것입니다.
Welch's t-test와 Student's t-test 사이의 주요 차이점은 자유도 (degrees of freedom) 와 표본 분산의 추정치 (sample variance estimates) 입니다. Student의 가정은 샘플이 같은 분산을 가진다고 가정하는 것이고 Welch's 는 그렇지 않습니다.
Welch's t-test 든 Student's t-test든 가설 검정에 사용되는 큰 표본의 크기를 비교할 때 (n > 10,000), 두 검정 법간의 신뢰수준의 차이는 일반적으로 무시할 수 있습니다. 큰 표본 크기를 다룰 때 스튜던트 t-검정의 등분산 가정이 검정의 정확도에 미치는 영향이 미미하기 때문입니다.
등분산 가정이 위배되더라도 스튜던트 t-검정은 정확한 p-값을 생성하고 원하는 유형 I 오류율(참 귀무가설을 기각할 확률)을 유지한다는 의미로 비교적 견고하게 유지됩니다. 이러한 강건성은 표본 크기가 증가함에 따라 표본 평균의 분포가 기저 모집단 분포에 관계없이 정규 분포에 접근한다는 중심 극한 정리(Central Limit Theorem)에 기인합니다.
이와 대조적으로, Welch's t-test는 특히 이분산성을 다루기위해 고안된 것으로, 등분산 가정이 의심스러울때 더 적합하게 만듭니다. 그러나 표본 크기가 크다면, Welch's t-test와 Student's t-test간의 신뢰수준의 차이는 근소합니다.
만약 이분산의 가능성에 대하여 염려가 된다면, Welch's t-test가 더 안전한 선택입니다. 하지만, 검정력을 최대화하고 표본 크기가 충분히 크다고 확신하는 경우 스튜던트 t-검정을 사용할 수 있습니다.
Bartlett’s test 을 사용하여 데이터의 등분산을 검정하는 방법은 아래 코드 스니펫을 참조하십시오. Bartlett’s test 은 정규성 가정을 필요로 하는 매우 강력한 검정입니다. 덜 강력한 검정을 선호한다면 Levene 검정이 더 적합할 수 있습니다.
Test for Equal Variances
from scipy.stats import bartlett, levene
# Perform Bartlett's test for equal variances (works best on data that conforms to normality)
statistic, p_value = bartlett(group_A, group_B)
# Perform Levene's test for equal variances (less sensitive to Normality assumption)
statistic, p_value = levene(group_A, group_B)
# Display test results
print(f"Test statistic: {statistic}")
print(f"P-value: {p_value}")
if p_value < alpha:
print("Reject the null hypothesis. There is a significant difference in variances between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference in variances between the groups.")
Flow 2b: 평균? 중앙값?
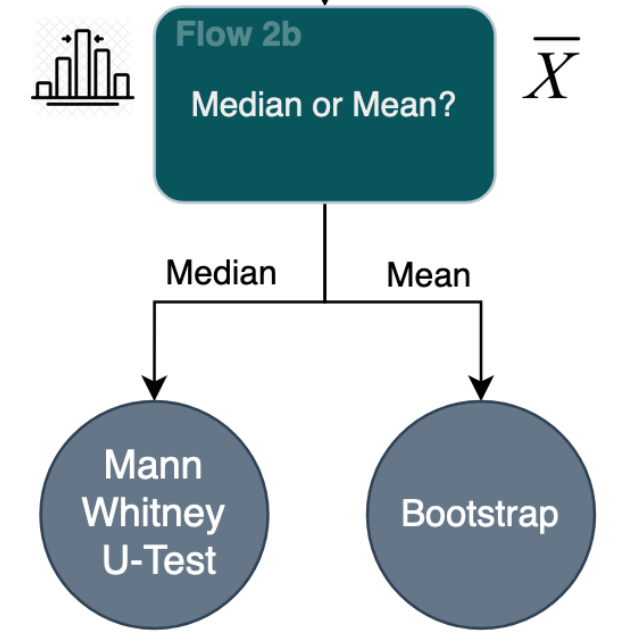
위의 Average Per User(사용자당 평균) Flowchart에서 이어집니다 -
데이터 세트가 정규성을 준수하는지에 대해 합리적인 의심이 있는 경우 데이터 세트를 분석하는 데 다른 통계적 방법이 더 적합할 수 있습니다. 다음 단계는 데이터의 평균 또는 중위수가 더 유용한지 여부를 결정하는 것입니다.
A/B 테스트에서 평균일지 중앙값 일지 고려하는 것은 특정 시나리오에서 유용할수 있습니다. 특히 아웃라이어나 정규 분포가 아닌 매우 치우친 분포에 의해 영향이 있을 수도 있는 데이터를 다룰 때는 그렇습니다.
- 결과 전달하기: 중앙값을 사용하면 특히 일반적이거나 일반적인 사용자당 행동을 설명할 때 중심 경향에 대한 보다 명확하고 직관적인 해석을 제공할 수 있습니다. 이해관계자 또는 비기술적인 사람들에게 더 관련성이 있을 수 있습니다.
- 치우친 분포: 데이터가 매우 치우쳐 있거나 정규 분포를 따르지 않는 경우 평균이 정규 분포를 정확하게 나타내지 못할 수 있습니다. 이 경우 중위수는 극단값이나 분포의 모양에 영향을 덜 받기 때문에 중심 경향에 대한 보다 강력한 추정치를 제공합니다.
- 아웃라이어 민감도 : 평균은 아웃라이어나 극단치 값에 매우 민감합니다. 몇 개의 이상치도 평균을 크게 왜곡하여 중심 경향의 대표성에 영향을 줄 수 있습니다. 이와 대조적으로, 중앙값은 순서대로 정렬을 했을 때 중앙 값을 의미하기 때문에 극단치에 덜 영향을 받습니다.
두 측정값 모두 장점이 있으며, 이 중에서 선택하는 것은 데이터의 특성, 이상치의 영향 및 A/B 검정에서 도출하려는 특정 통찰력과 일치해야 합니다. 결론을 내릴 때 평균과 중위수를 모두 고려해야 합니다.
이것은 Mann-Whitney U Test와 관련된 매우 유용한 가이드 입니다.
항상 그렇듯 테스트에 뛰어들기 전에 각 테스트를 철저히 이해하기 위한 조사를 하는 것이 가장 좋습니다!
통계적 검정 (Statistical Tests)
위의 사용자당 평균 플로우차트를 따랐다면, 이제 두 그룹의 지표가 통계적으로 유의미한지 여부를 판단하는 가장 좋은 검정 기법이 무엇인지 결정했을 것이다. 아래의 테스트을 수행하는 방법을 참조하십시오.
위의 GUIDE 및 Average Per User 흐름도를 참조하십시오.
Student’s t-test
import scipy.stats
# Student's t-test - This test requires Normality and Equal Variances
t_statistic, p_value = stats.ttest_ind(group_A, group_B)
print(f"Student's t-test: t = {t_statistic}, p-value = {p_value}")
if p_value < alpha:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
Welch’s t-test
import scipy.stats
# Welch's t-test - This test requires Normality
t_statistic, p_value = stats.ttest_ind(group_A, group_B, equal_var=False)
print(f"Welch's t-test: t = {t_statistic}, p-value = {p_value}")
if p_value < alpha:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
Mann-Whitney U-test
# Mann-Whitney U-test - No statistical assumptions, Median preferred over Mean
u_statistic, p_value = stats.mannwhitneyu(group_A, group_B)
print(f"Mann-Whitney U-test: U = {u_statistic}, p-value = {p_value}")
if p_value < alpha:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
Bootstrapping
(부트스트랩 순열 검정법)
#Bootstrapping - forNon-Normal data/Small sample sizes, and Mean is preferred
# Calculate observed difference in means
observed_diff = np.mean(group_B) - np.mean(group_A)
# Combined data
combined_data = np.concatenate((group_A, group_B))
# Number of bootstrap samples
num_samples = 10000 # You can adjust this number based on computational resources
# Bootstrap resampling
bootstrap_diffs = []
for _ in range(num_samples):
# Resample with replacement
bootstrap_sample = np.random.choice(combined_data, size=len(combined_data), replace=True)
# Calculate difference in means for each bootstrap sample
bootstrap_mean_A = np.mean(bootstrap_sample[len(group_A):])
bootstrap_mean_B = np.mean(bootstrap_sample[:len(group_A)])
bootstrap_diff = bootstrap_mean_B - bootstrap_mean_A
bootstrap_diffs.append(bootstrap_diff)
# Calculate p-value (significance level)
p_value = np.mean(np.abs(bootstrap_diffs) >= np.abs(observed_diff))
print(f"P-value: {p_value}")
if p_value < alpha:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
부트스트랩 순열검정 리마인드
우리는 서비스를 개선시키기위해 혹은 유저경험을 개선시키기 위해서 A/B테스트를 많이 진행하게 된다. 이때 우리는 실험의 결과가 우연에 의한 차이는 아닌지 의심하게 된다. 많은 경우에 t검
velog.io
Section 2 : 범주형 지표 Categorical Metrics
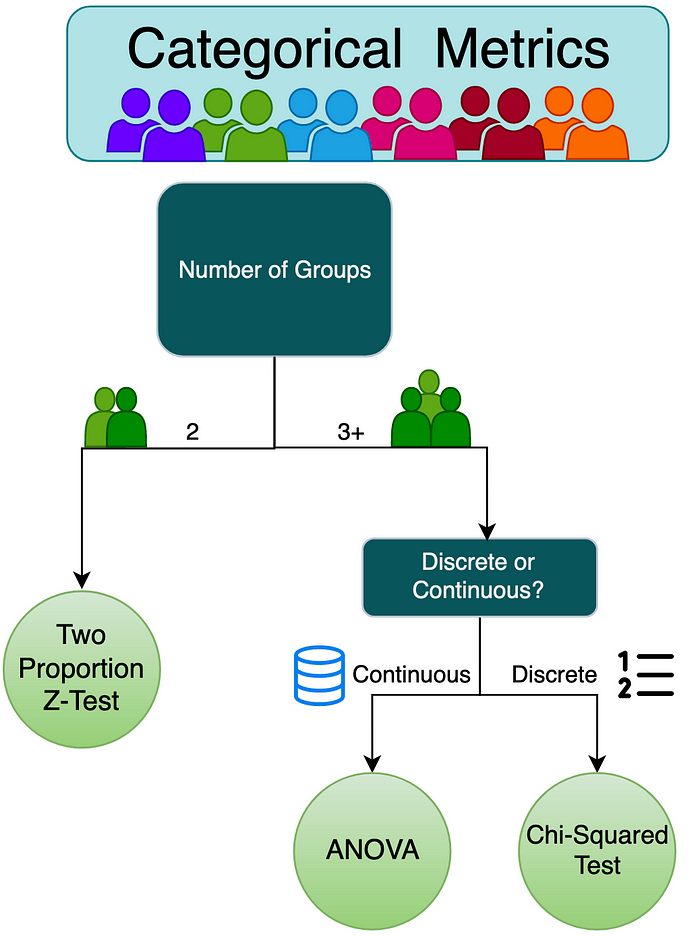
이번 섹션에서는 범주형 지표에 대해 탐구해볼 것입니다. 이 지표는 클릭/미클릭 과같은 이산변수가 될 수도 있고, 다변량 기법과 같은 연속형일 수도 있습니다.
당신의 데이터에 맞는 최적의 검증기법을 위 플로우 차트에 따라 선택하세요.
2 Groups
Two Proportion Z-test (Binary Metrics)
리텐션, 전환율, 클릭률 과같은 지표들을 의미합니다.
AB테스트의 이항 변수에 대한 two-sample z-test 는 두 그룹사이의 이진 결과에 대한 비율을 비교합니다. 통계적인 관점에서 이항 분포는 N이 크면 클수록 정규분포에 수렴합니다. 이 가정은 일반적으로 잘 맞아 z-test를 사용하는 것이 합리적입니다.
H0:μ1−μ2=0
HA:μ1−μ2≠0
Two proportion Z-test
from statsmodels.stats.weightstats import ztest
# Calculate the z-statistic and p-value. This assumes binomially distributed and i.i.d. variables.
z_stat, p_value = ztest(group_A, group_B)
print(f"Two Sample z-test: t = {z_stat}, p-value = {p_value}")
if p_value < alpha:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
3+ Groups
Discrete Variables
Pearson's Chi-Squared Test
카이스퀘어 검정은 특히 대조군에 대하여 다수의 그룹을 가졌을 때, A/B 테스트를 분석하는데 강력한 도구입니다.
이 기법은 분포 속성을 가정하지 않고 여러 대조군을 동시에 비교할 수 있습니다. 이 방법은 또한 위와 유사한 이진 변수로 작동하지만 단지 2개가 아닌 여러 그룹을 사용할 것입니다. 이들 그룹은 표본 크기를 더 작은 그룹으로 분할할 가능성이 있으므로, 각 그룹에 대한 표본 크기가 비교적 크게 유지되도록 하는 것이 중요합니다.
Pearson의 Chi Sq Test를 이용하여 여러 그룹 간에 범주형 데이터의 관측 빈도와 예상 빈도 간에 유의한 연관성 또는 차이가 있는지 확인합니다. 그리고, 그룹간의 차이가 없다는 귀무가설을 가정합니다.
데이터가 이산적이라면, 각 대조군들에 대하여 갯수를 합친 결합 테이블을 만들 수 있습니다. 이것은 stats.chi2_contingency 함수로 해석될 수 있습니다.
Pearson’s Chi-Squared Test
Create a contingency table
contingency_table = pd.crosstab(df['Variant'], df["metric"])
# Perform the chi-squared test
chi2, p_value, dof, expected = stats.chi2_contingency(contingency_table)
if p_value < alpha:
print("There is a statistically significant difference in the distribution of the metric across groups.")
else:
print("There is no statistically significant difference in the distribution of the metric across groups.")
Continuous Variables
ANOVA Test
ANOVA는 3개 이상 그룹의 평균을 비교할때 사용하는 통계적 기법입니다. 그룹 평균 간의 관찰된 차이가 우연에 의한 것인지 아니면 실제로 기본 모집단에서 유의한 차이를 나타내는지 평가합니다. 서로 다른 여러 변인을 출시할 때 유용하며 개별 A/B 테스트를 배포하는 것보다 결과를 서로 비교하여 시간을 절약하고자 합니다.
ANOVA 분석은 정규성 및 분산 동질성 가정의 위반에 상대적으로 강건하며, 특히 표본 크기가 상당히 큰 경우에는 더욱 그러합니다.
ANOVA Test
# Group the counts for the various groups in the data
grouped_data = [df[df['Variant'] == cat]['Metric'] for cat in df['Variant'].unique()]
# Perform ANOVA test
f_statistic, p_value = stats.f_oneway(*grouped_data)
if p_value < alpha:
print("There is a statistically significant difference in the means of the metric across groups.")
else:
print("There is no statistically significant difference in the means of the metric across groups.")
이 테스트는 그룹간이 통계적으로 유의미한 차이가 있는지를 결정합니다. 여기서 우리가 마주치게될 한가지 문제는 나머지 보다 훨씬 좋은 결과를 낸 특정 그룹을 식별하려고 하는것입니다. 집단 분산 분석 검정은 일반적인 편차를 강조하지만, 다른 그룹에 비해 통계적 차이를 보이는 특정 그룹을 식별하기 위해서는 더 깊은 조사가 필요합니다.
다행히도, 체계적인 방식을 제공하는 Turkey's range test를 사용하는 깔끔한 함수가 있습니다. 모든 집단 조합에 걸쳐 종합적인 쌍대 비교표를 생성하여 그들 간의 통계적으로 유의미한 차이를 드러냅니다.
그러나 Turkey's range test 에서 기본 가정을 위반할 가능성이 있으므로 주의를 기울여야 한다. 이 검사는 주로 그룹 비교에서만 지원 도구로 사용하여 서로 다른 그룹을 식별하는 데 사용되어야 한다. 이것은 그것이 어떻게 수행되고 사용되는지를 보여주는 정말 유용한 비디오입니다.
나머지를 능가하는 특정 그룹을 식별하려면 위의 ANOVA 테스트에 도움이 되는 코드 스니펫을 참조하십시오.
Turkey’s HSD test
import statsmodels.api as sm
from statsmodels.stats.multicomp import pairwise_tukeyhsd
# Perform Tukey's HSD test for post-hoc analysis
tukey = pairwise_tukeyhsd(df["metric"], df['Variant'])
# Print pairwise comparison results
print(tukey.summary())
Section 3 : 결합 지표 Joint Metrics
위의 가이드에 따라 메트릭이 실제로 2개 이상의 변수로 구성된 공동 메트릭임을 확인한 경우, 여러 그룹 간의 통계적 차이를 효과적으로 파악하기 위해 추가 조치를 취해야 할 수 있습니다. 위의 다른 테스트에서는 테스트하는 메트릭이 서로 독립적이라고 가정하기 때문입니다.
Delta t-test
Delta t-test는 두 개의 확률 변수가 결합 분포를 형성하는 비율을 고려하면서 두 개의 독립적인 그룹 간의 평균 차이를 평가하기 위해 사용되는 통계 방법입니다. A/B 테스트의 영역에서는 메트릭 자체가 독립적이지 않을 수 있는 시나리오가 종종 존재한다.
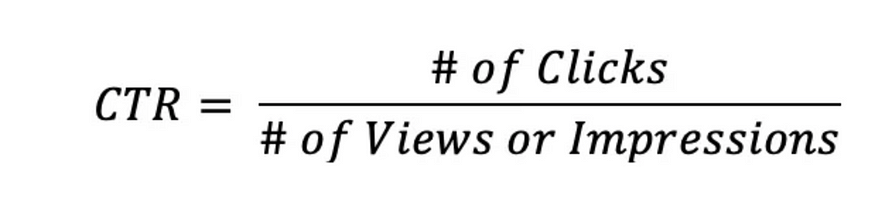
한 예로 클릭률이 있습니다. 한 사람이 같은 광고를 여러번 볼 수 있지만 클릭은 한번 발생합니다.
여기서 표준 t-검정을 사용할 때의 문제는 우리가 두 개의 개별 확률 변수를 분석하고 있고, 그 비율이 결합 분포를 형성한다는 것입니다. 사용자들 자체는 독립적이지만 결합 비율은 그렇지 않습니다. 이는 Student's and Welch's t-test의 독립성 가정에 위배됩니다.
대신 델타 방법을 사용하여 분산을 추정합니다;
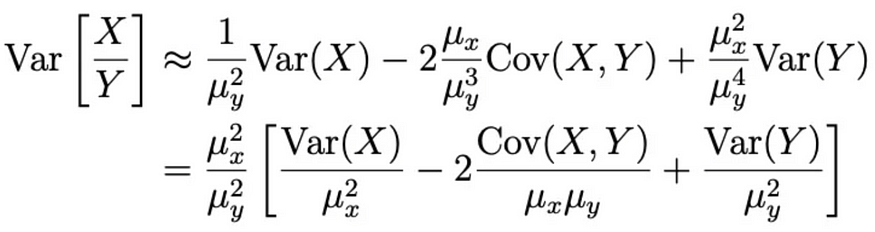
이 새로운 분산 공식을 계산하는 방법과 이 새로운 분산을 사용하여 t-검정 함수를 만드는 방법을 보여주는 코드 스니펫을 참조하십시오.
Delta t-test
# create the new Variance function as described above
def var_ratio(metric1,metric2):
mean_x = np.mean(metric1)
mean_y = np.mean(metric2)
var_x = np.var(metric1,ddof=1)
var_y = np.var(metric2,ddof=1)
cov_xy = np.cov(metric1,metric2,ddof=1)[0][1]
result = (mean_x**2 / mean_y**2) * (var_x/mean_x**2 - 2*cov_xy/(mean_x*mean_y) + var_y/mean_y**2)
return result
# create this new ttest function, using the new Variances above. This is a standard t-test function.
def delta_ttest(mean_c,mean_t,var_c,var_t, alpha = 0.05):
mean_diff = mean_t - mean_c
var = var_c + var_t
std_e = stats.norm.ppf(1 - alpha/2) * np.sqrt(var)
lower_ci = mean_diff - std_e
upper_ci = mean_diff + std_e
z = mean_diff/np.sqrt(var)
p_val = stats.norm.sf(abs(z))*2
return z, p_val, upper_ci, lower_ci
#Eg. Here we calculate the significance of the CTR for a control and treatment group.
var_c = var_ratio(control['click'],control['view']) #Calculates the delta variance for the control group
var_t = var_ratio(treatment['click'],treatment['view']) #Calculates the delta variance for the treatment group
mean_c = control['click'].sum()/control['view'].sum()
mean_t= treatment['click'].sum()/treatment['view'].sum()
z, p_value, upper_ci, lower_ci = delta_ttest(mean_c,mean_t,var_c,var_t,alpha) #Applies the ttestusing these new delta variances
if p_value < alpha:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
결론:
요약하면, A/B 검정은 실험과 최적화에 매우 귀중하지만, 올바른 통계 검정의 선택은 필수적이다. 강력하고 신뢰할 수 있는 결과를 위해서는 데이터 과학자들이 특성과 검정 가정을 신중하게 고려해야 한다.
A/B 테스트는 강력한 도구이지만 잘못된 통계 테스트를 선택하면 오해의 소지가 있는 결과를 초래할 수 있다는 것을 기억하세요!
References:
1. Test for Normality by Sivasai Yadav Mudugandla
2. Levene’s Test by Kyaw Saw Htoon
3. Mann Whitney U Test by Ricardo Lara Jácome
4. Delta Method: https://arxiv.org/pdf/1803.06336.pdf
'노트 > Data Science : 데이터과학' 카테고리의 다른 글
| MMM (Marketing Mixed Modeling) (0) | 2024.08.23 |
|---|---|
| Complete Guide to A/B Testing Design, Implementation and Pitfalls (0) | 2024.07.05 |
| [Regression and Prediction] 판매에서 광고의 효과 (0) | 2024.05.07 |
| [Unstructured Data] 고객 클러스터링 (0) | 2024.05.03 |
| [Regression and Prediction] 부트스트랩핑 (Bootstrapping) (0) | 2024.05.03 |