노트/Data Science : 데이터과학

Complete Guide to A/B Testing Design, Implementation and Pitfalls

Diane_ 2024. 7. 5. 21:10

https://news.lunartech.ai/simple-and-complet-guide-to-a-b-testing-c34154d0ce5a

Simple and Complete Guide to A/B Testing

End-to-end A/B testing for your Data Science experiments for non-technical and technical specialists with examples and Python…

news.lunartech.ai

A/B 테스팅 설계, 구현과 함정에 대한 완벽 가이드

예제와 python 구현과 함께, 비 기술직군 과 기술직군 전문가를 위한 데이터 과학 실험에 대한 A/B 테스팅의 End-to-end

A/B 테스팅은 통계학자들 사이에서 무작위 통제 실험으로 부터 유례된 split testing 이라고도 불리며, 당신의 비즈니스가 새로운 프로덕트 또는 피쳐들을 실행해야할지 말지를 결정하기 위해 비즈니스에서 새로운 UX 기능들과 프로덕트 또는 알고리즘의 의 뉴버전을 테스트 해보는 가장 유명한 방법들 중 하나이다.

“The world is a big A/B test”
Sean Ellis

이 글은 A/B 테스트를 수행할 때 고려해야하는 주제들을 다뤄야하는 기술적 비기술적 독자들을 위해 작성했다.

- A/B 테스트는 무엇이고 언제 사용해야하는가?
- A/B 테스트 전에 명확하게 해야할 질문
- 주요 지표 선택
- 가설 검정
- 테스트 설계 (검정력 분석)
- 표본 크기, 테스트 기간 계산
- 통계적 검정 ( T-test, Z-test, Chi-squared test)
- Python에서 A/B 테스트 결과 분석
- SE(표준오차) 와 CI(신뢰구간)에 대한 부트스트래핑과 부트스트랩 분위수 방법
- 통계적 유의성 VS 실제적 유의성
- A/B 테스트의 품질 (신뢰성(reliability), 타당성(validity), 유효성(potency))
- A/B 테스트의 공통 문제와 함정
- A/B 테스팅의 윤리와 프라이버시
- LunarTech에서 제공하는 A/B 테스트 과정

만약, 사전에 통계학 지식이 없다면, 간단히 통계적 유도와 공식을 생략할 수 있습니다. 그러나, 필수 통계 개념에 대한 지식을 리프레쉬 하거나 배우길 원한다면, 이 글을 확인하면 됩니다: Data Scientists와 Data Analysts를 위한 통계 기초

A/B 테스트는 무엇이고 언제 사용해야 하는가?

A/B 테스팅에 대한 배경은 고객 표본(실험 그룹) 에게 제품의 변형 버전을, 다른 고객 표본(대조군)에게 제품의 기존 버전을 보여준다는 것입니다. 그러면, 실험군/대조군 간의 제품 성능의 차이가 추적되고, 프로덕트의 성능에 대한 제품의 새로운 버전에 대한 효과를 식별하게 됩니다. 그래서, 테스트 기간동안의 지표를 추적하고, 제품 성능의 차이가 있는지 확인하고 차이가 무엇인지 확인하는 것이 목표입니다.

이 테스트 배경의 모티브는 기존 제품의 성능을 향상시키고, 이 제품을 더욱 성공적이고 최적화 시켜서 긍정적인 효과를 보여줄 신제품의 변화를 테스트 하는것입니다.

이 테스팅을 좋게 만드는 것은 비즈니스들이 그들의 실제 고객들로 부터 기존 버전과 변화된 제품/특징을 옵션으로 제공함으로써 직접적인 피드백을 얻는 것입니다. 그리고 이런 방식으로 새로운 아이디어들을 빠르게 테스트해볼 수 있습니다. A/B 테스트에서 변형 버전/접근 방식이 효과적이지 않다는 것을 알 수 있는 경우, 적어도 기업은 이를 통해 학습하고 개선이 필요한지 아니면 다른 아이디어를 찾아야 하는지 결정할 수 있습니다.

A/B 테스팅의 이점

무엇이 효과적인지, 무엇이 그렇지 않은지를 빠른 방법으로 학습할 수 있습니다
실제/진짜 제품의 고객들로부터 직접적인 피드백을 얻습니다.
유저가 테스트되고있다는 사실을 인식하지 못하기 때문에, 결과가 편향되지 않습니다.

A/B 테스팅의 단점

특히 같은 지리적 위치에 있는 다른 고객들에게 다른 콘텐츠/가격/특징들을 보여주는것은 잠재적으로 위험할 수 있으며, 이로 인해 변경 회피가 발생할 수 있습니다. (나중에 이 문제를 어떻게 다룰 수 있는지 논의해볼 것입니다.)
상당한 양의 제품, 엔지니어링, 데이터 사이언스 리소스가 요구됩니다.
제대로 수행되지 않으면 잘못된 결론을 도출할 수도 있습니다.

이 테스트 배경의 모티브는 기존 제품의 성능을 향상시키고, 이 제품을 더욱 성공적이고 최적화 시켜서 긍정적인 효과를 보여줄 신제품의 변화를 테스트 하는것입니다.

A/B 테스트 전에 명확하게 해야할 질문

A/B 테스트가 상당한 리소스 양이 필요하고, 상당한 영향을 주는 제품 결정을 초래한다는 점을 고려해보았을 때, 테스트에 뛰어들기 전에 당신 스스로에게도, 상품팀, 엔지니어링팀, 그리고 몇몇 주요한 질문을 하는 상황과 관계있는 다른 이해관계자들에게 의견을 물어보는 것은 꽤 중요합니다.

표본 모집단은 어떠하며, 대상 제품의 고객 세그먼트는 무엇인가요?
탐색적/히스토리 데이터 분석을 사용하여 비즈니스 질문에 대답을 찾을 수 있나요? (e.g 인과 추론 분석을 사용)?
타겟 제품의 하나 또는 다수의 변형군들을 테스트하길 원하나요?
정말 랜덤된 통제군과 실험군을 확실할 수 있나요? 즉, 두 표본이 비편향되고, 진짜 사용자 집단을 대표하나요?
전체 시험 기간 동안 처치 효과와 통제 효과의 무결성을 확실할 수 있나요?

A/B 테스팅의 목표는 테스트 기간 동안 주요 지표를 추적하여 제품 성능에 차이가 있는지, 차이의 유형이 무엇인지 밝혀내는 것입니다.

A/B 테스트를 위한 주요 지표 선택

지표를 선택하는 것은 A/B 테스트의 가장 중요한 부분중 하나입니다. 왜냐하면 이 지표가 실험군과 대조군들에 대한 제품이나 기능의 성과를 측정하고, 이 두 그룹간에 통계적으로 유의미한 차이가 있는지 식별할 때 사용되기 때문입니다.

성공적인 지표 선택은 A/B 테스트로 실험이 진행되고 있는 가설에 영향을 받습니다. 이것은 A/B 테스트의 가장 중요한 부분 중 하나이지만, 테스트가 어떻게 설계될 것인지, 또한 제안된 아이디어가 얼마나 잘 수행될 것인지를 결정하기 때문입니다. 잘못된 메트릭을 선택하면 많은 작업이 수행되지 않거나 잘못된 결론을 내릴 수 있습니다.

수익이 항상 최종 목표는 아니기 때문에, A/B 테스트를 위해서는 제품의 직접적인 목표와 더 높은 수준의 목표에 기본 메트릭을 연결해야 합니다. 기대하는 바는 제품이 더 많은 돈을 벌면, 컨텐츠가 훌륭하다는 것을 시사한다는 것입니다. 하지만, 이 목표를 달성하는 것에 있어 자료와 글의 전반적인 내용을 개선하는 대신 퍼널 전환율을 최적화할 수 있습니다. A/B 테스트에서 당신이 선택한 지표의 정확성을 테스트하는 한가지 방법은 당신이 풀고자 하는 정확한 문제로 되돌아가는 것이 될 수 있습니다. 당신 스스로에게 다음의 질문을 해보세요:

지표 유효성 질문: 모든 것이 동일한 상황에서 선택된 지표가 증가한다면, 우리의 목표를 달성하거나 문제를 해결할 수 있는가?

당신의 A/B 테스트를 위해 하나의 주요 지표를 선택할 필요가 있음에도 불구하고, 여전히 남아있는 지표들을 주시하여 타겟 지표 뿐만 아니라 모든 지표들이 변화를 보였는지 확실히할 필요가 있다. A/B 테스트에서 여러 개의 지표를 사용하면 효과가 없는 동안 많은 중요한 차이를 식별할 수 있기 때문에 오탐이 발생할 수 있으며, 이는 피하고 싶을 것입니다.

A/B 테스트의 공통 지표

A/B 테스트에서 자주 사용되는 잘 알려진 성과 지표는 클릭률, 클릭 확률, 전환율이 있다.

1: 사용에 대한 클릭률 (Click-Through Rate (CTR))

전체 뷰 또는 세선 수를 고려했을 때, 이 수치는 페이지를 보고 (impressions) 실제로 클릭한 (clicks) 사람들의 퍼센테이지 수치를 의미한다.

2: 영향에 대한 클릭확률 (Click-Through Probability (CTP))

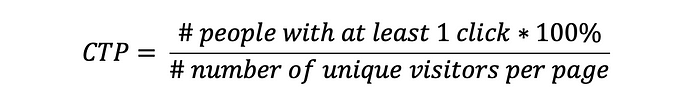
CTR과는 달리, CTP는 사용자가 한 세션 동안에 같은 아이템에 어떤 이유로 중복 클릭을 했다면, (예를 들어, 조급함 때문에), CTP 에서는 이 다수의 클릭을 하나의 클릭이라 고려한다.

CTP를 계산하기 위해서, 웹사이트를 수정하기 위해 엔지니어와 협력할 필요가 있습니다. 모든 페이지뷰에 대해 view/impression 이벤트를 캡쳐하고, 각 페이지 뷰를 페이지당 모든 자식 클릭 수와 일치시켜 고유한 페이지 뷰당 하나의 자식 클릭 수만 계산되도록 합니다.

3: 전환률 (Conversion Rate)

전환율은 세션이 트랜잭션으로 끝나는 비율로 정의됩니다.

따라서, 사이트의 사용성을 측정할려면 CTR을 사용하고, 기능의 실제 영향을 측정하려면 CTP를 사용할 수 있습니다. CTR은 중복 클릭을 고려하지 않기 때문에, 유저가 같은 버튼을 여러번 조급하게 클릭하면, 정확하게 1과 같도록 수정되지 않습니다.

가설검정 시작하기

A/B 테스트는 항상 테스트될 가설을 기반으로 합니다. 관련있는 상품 팀과 데이터 사이언스 팀의 브레인스토밍과 협업의 결과로 수립됩니다. 이 가설의 배경은 이러한 문제의 해결책이 관심 있는 주요 성능 지표(KPI)에 영향을 미치는 제품의 잠재적 문제를 어떻게 '수정'할 것인지 결정하는 것입니다.

이것은 제품의 문제와 테스트할 아이디어의 범위에서 우선순위를 정하는 것은 매우 중요하며, 문제를 선택하고자 할 때 이 문제를 해결하는 것이 제품에 가장 큰 영향을 미칠 것입니다.

예를 들어, 제품의 KPI가 추천 시스템의 추천 결과의 품질을 향상시키는 것이라면, 추천인에 대해 인상 할인을 추가하거나, Re-ranker 모델을 구축하여 수행될 수 있습니다. 그러나 이 두 해결책의 영향은 추천사항의 품질 향상 정도에 따라 다를 것으로 보입니다. 즉, re-ranker 모델은 이전에 사용자에게 제시해준 추천사항을 사용자가 보지 못하도록 하는 인상 할인과 달리, 사용자에게 제시된 추천의 세트를 잠재적으로 변경함으로써 추천의 순위에 영향을 미칩니다.

이 특별한 예시에 따라, 타겟 추천시스템의 품질을 향상시키기를 기대하는 re-ranked 모델을 만들기로 결정할 수 있습니다. (이 가상의 추천 시스템을, RecSys 라 합시다). 추가적으로, XGBoost가 RecSys의 추천 사항의 순위를 다시 매기기 위한 re-ranker 모델로 사용될 수 있음을 확인한 연구를 수행했습니다.

마침내, 탐색적/ 오프라인 테스트 분석을 수행하여 추천 사항 품질의 향상을 확인하였습니다. (NDCG를 추천 품질의 성능 지표로 사용했다고 합시다) 그리고 상당한 영향력을 확인했습니다. 그래서, 마지막 확인으로, 이 XGBoost re-ranker가 RecSys 추천의 품질에 미치는 효과를 기존 버전의 추천과 비교하여 테스트하려고 합니다. 따라서 우리는 다음과 같은 가설을 세울 수 있습니다:

가설: 기존 RecSys 추천기에 XGBoost re-ranker 모델을 추가하면 추천시스템의 CTR이 증가할 것이며, RecSys 추천 시스템의 품질이 향상될 것이다.

여러 아이디어를 하나의 가설로 병합하지 말고 개별적인 영향을 파악할 수 있도록 테스트에 도입된 변수를 제한하세요. 그렇지 않으면, 당신의 테스트 끝에는 많은 질문들과 거의 없는 답변들만 남을 것입니다.

A/B test 설계하기

어떤 사람들은 A/B 테스트가 하나의 기술이라고 주장하고, 다른 사람들은 그것이 비즈니스로 조정된 흔한 통계 테스트라고 말합니다. 하지만 경계선은 이 실험을 제대로 설계하기 위해서는 실제로 실험을 하는 것이 아니라는 것을 염두에 두면서 훈련과 의도가 있어야 한다는 것이 다른 점입니다. - learning 에 대한 것입니다.
다음은 A/B 테스트를 위한 확실한 디자인을 갖추기 위해 취해야 할 단계입니다.

Step 1: Statistical Hypothesis (통계적 가설 수립)

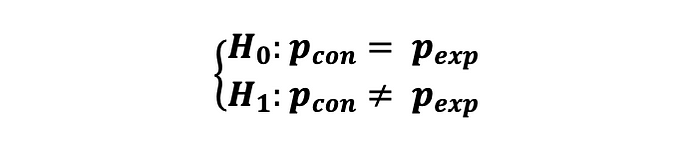
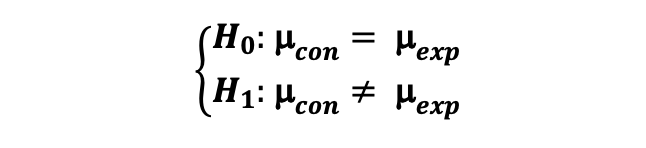
Step 2: Power Analysis (검정력 분석)

우리의 테스트가 반복 가능하고, 견고하며, 전체 모집단에 대하여 일반화 될 수 있는지 확인하기 위해, 우리는 p-hacking 을 피하고, 실제 통계적인 유의성을 보장하며, 편향된 결과를 피하기 위해 "충분한" 양의 관측치를 수집하고 미리 결정된 시간 동안 테스트를 실행하려고 합니다. 그래서, 테스트를 수행하기 전에 우리는 대조군과 실험군의 표본 크기를 결정해야 하고, 얼마나 오랫동안 테스트를 수행할지 기간을 결정해야 합니다. 이 과정은 Power Analysis 라고 종종 불리우고 3가지 특별한 단계를 포함합니다 : 테스트의 검정력을 결정하고, 테스트의 유의 수준을 결정하고, 발견가능한 최소 효과를 결정합니다. A/B 테스트 검정을 위한 검정력 분석에 관련된 매개 변수에 대한 일반적인 언급은 다음과 같은 표기법을 따릅니다:

Power of the test

통계적 검정력은 정확하기 귀무가설을 기각할 확률을 의미합니다. 검정력은 귀무가설이 거짓일 때, (귀무가설을 기각하는) 정확한 결정을 하는 확률입니다.

(1-beta) 로 정의가 되는 검정력은 type Ⅱ 오류를 만들지 않을 확률과 동일한데, Type Ⅱ 오류는 귀무가설이 거짓임에도 귀무가설을 기각하지 않을 확률입니다.

A/B 검정의 검정력으로 80%를 선택하는 것이 일반적인데, 즉 20%가 Type II 오류이며, 이는 효과가 있는 동안 처치 효과를 감지하지(null을 거부하지 못함)하지 않아도 괜찮다는 것을 의미합니다. 그러나, 이 매개변수 값의 선택은 테스트의 특성과 비즈니스 제약에 따라 달라집니다.

Significance level of the test

Type I 오류의 확률인 유의 수준은 귀무가설은 참이고 통계적으로 유의한 영향이 없지만, 귀무가설을 기각하여 처치 효과를 감지하는 가능성에 대한 확률을 의미합니다. 흔히 그리스 문자 알파, α로 정의되는 이 값은 종종 거짓 양성률이라고 불리는 거짓 발견을 할 확률입니다.

일반적으로, 실험군과 대조군 성능에 실제 차이가 없을 때 통계적으로 유의한 차이가 있다는 결론을 내릴 위험이 5%임을 나타내는 유의 수준의 값인 5%룰 사용합니다. 그래서, 100개의 케이스중에 5개가 실제로는 효과가 없음에도 처치 효과를 탐지해도 괜찮습니다. 또한 95% 신뢰에서 대조군과 실험군 간에 유의한 결과 차이가 있음을 의미합니다.

우리의 검정력 테스트의 케이스와는 달리, alpha 값의 선택은 테스트 본질과 비즈니스 제약에 의존합니다. 예를 들어, 만약 A/B 테스트를 수행하는 것이 높은 엔지니어링 비용과 관련이 된다면, 처치 효과를 탐지하기 쉽도록 높은 alpha 값을 고선택하도록 결정할지도 모릅니다. 반면에, 제품에서 제안된 버전의 구현 비용이 높다면, 높은 구현 비용을 정당화 하기 위해 제안된 기능이 진짜 큰 영향을 미쳐 귀무가설을 기각하기가 더 어려워 지기 때문에 낮은 신뢰 수준 값을 선택할 수도 있습니다.

Minimum Detectable Effect (delta)

비즈니스 관점에서, 기업이 이 개선사항을 투자 가치가 있다고 판단하기 위해 새로운 버전의 최소 영향으로 보고 싶어하는 통계적 유의성에대한 실질적인 의미는 무엇일까?

이 질문에 대한 답은 새로운 버전의 지표에서 기존 버전과 비교하여 어떤 형태로든 변화를 관찰하여 이 기능이 제품에서 시작되어야 하는지 비즈니스에 대한 권장 사항을 제시하는 것입니다. 이 매개변수의 추정치는 그리스 문자 delta로 정의되는 최소 검출 가능 효과 (Minimum Detectable Effect)로 알려져 있으며, 이는 테스트의 실질적인 중요성과도 관련이 있습니다. MDE는 비즈니스에 실질적으로 중요한 최소효과와 관련된 proxy이며, 일반적으로 이해 관계자에 의해 설정됩니다.

https://splitmetrics.com/resources/minimum-detectable-effect-mde/

Minimum Detectable Effect (MDE) • SplitMetrics

1. What is the Minimum Detectable Effect (MDE)? It’s a minimum improvement over the conversion rate of the existing asset (baseline conversion rate) that you want the experiment to detect. By setting MDE, you define the conversion rate increase suffici

splitmetrics.com

A/B 검정의 유의수준은 5%로, 80%를 검정력으로, 즉 Type II 오차 20%와 Type I 오차 5% 로 선택하는 것이 일반적이다. 그러나 이 모수의 값 선택은 검정의 특성과 비즈니스 제약에 따라 달라진다.

Step 3: Calculating minimum sample size (최소 표본 크기 산출)

A/B 테스트의 또다른 중요한 부분 중 하나는 검정력 검정 (1-beta), 유의수준 (alpha), 최소 검출 효과 (MED), 그리고 동일한 크기의 정규 분포된 두 표본의 분산을 결정하기 위해 사용이 필요한 통제군과 실험군의 최소 표본 크기를 결정하는 것입니다. 표본 크기의 결정은 통제군과 실험군의 진행상황을 추적하기 위해 선택한 주요 지표를 결정하는 것에 의존합니다. 여기서 우리는 두 케이스를 구분합니다. 첫번째 케이스는 A/B 테스트의 주요 지표가 이항 변수의 형태인 것입니다. (예를들어 클릭 or 미클릭) 그리고 두번째 케이스는 주요 지표가 비율이나 평균의 형태인 것입니다. (예를 들어 주문량 평균)

https://www.evanmiller.org/ab-testing/sample-size.html

Sample Size Calculator

Visual, interactive sample size calculator ideal for planning online experiments and A/B tests.

www.evanmiller.org

Case 1: 이항 지표에 대한 표본 크기 계산

사용자가 클릭 (성공) 또는 미클릭 (실패) 했는지에 대한 클릭률과 같은 두가지 가능한 값에 관련된 지표를 주된 성과로 트래킹 하고자 할 때나 사용자의 제품에 대한 반응이 "독립적"으로 정의가되어 베르누이 시도로 고려할 수 있는 경우를 다뤄보고자 한다. 베르누이 시도의 예로는 클릭 이벤트 (성공) 이 통제 집단에서 p_con 의 확률로 발생하고, 실험 집단에서 p_exp 확률로 발생하는 경우를 의미한다. 이외에도 미클릭 이벤트 (실패)는 통제집단에서 q_con 의 확률로 발생하고 실험군의 집단에서 q_exp 확률로 발생한다. :

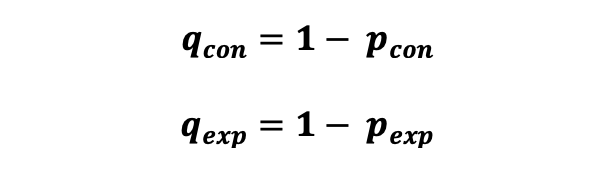
이에 따라, 성공의 횟수로 묘사된 랜덤 확률 변수는 (클릭) 다음의 이항 분포를 따르는 것으로 고려될 수 있으며, 이 분포에서 표본 크기는 사용자에게 노출된 기능/제품의 수가 되며 성공 확률은 통제군과 실험군 각각 p_con 과 p_exp 이다. 그런 다음 사전 지정된 유의 수준, 검정력 수준, MID를 사용하여 이 두 이항 비율을 비교하는 데 필요한 표본 크기를 다음과 같이 계산할 수 있습니다:

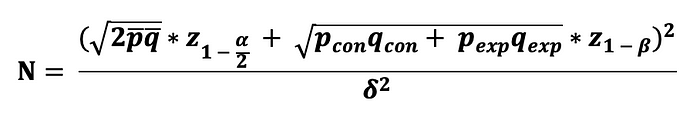
여기에서 p_bar와 q_bar의 추정치를 얻기 위해서 A/A testing (두 그룹에 동일한 처치를 하는 A/B 테스트) 가 필요합니다.

Case 2: 연속형 지표에 대한 표본 크기 계산

통제군과 실험 군의 평균을 비교하기 위해 평균 주문량과 같은 형태의 지표를 주된 성과로 트래킹하고자 할 때, 중심 극한 정리에 의해 두 통제군과 실험군의 표본 분포의 평균은 정규 분포를 따른다고 할 수 있다. 그에 따라 이 두 그룹의 평균 차이는 정규 분포를 따른다. 즉 :

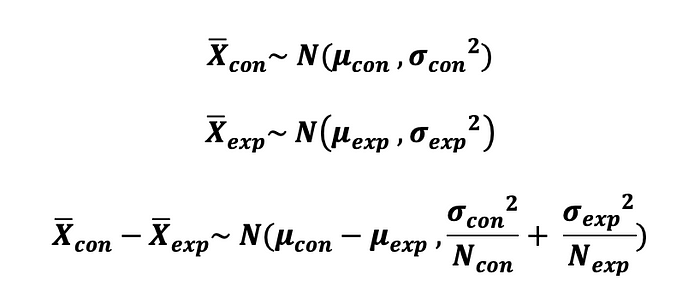
그래서, 두 정규 분포 표본의 평균을 비교하기 위해 필요한 표본의 크기는 사전에 정의된 신뢰수준, 검정력, MID를 사용하여 다음과 같이 계산할 수 있다. :

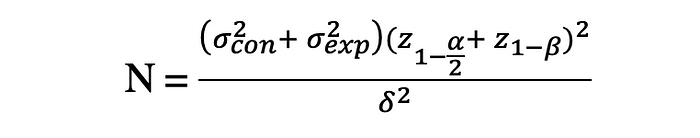
여기서, 표본 분산 $\sigma^2_{con}$ 와 $\sigma^2_{exp}$ 를 얻기 위해 A/A test를 수행할 수 있다.

테스트 기간 동안 유저로 부터 얻은 성공(클릭)의 수는 이항 분포를 따르며 표본 크기는 기능/제품이 사용자에게 노출된 횟수이고 성공의 확률은 통제군과 실험군 각각 p_con, p_exp 이다.

Step 4: Determining A/B test duration (A/B 테스트 기간 결정)

앞서 언급했듯이, 이 질문은 통계적 유의성을 감지했을 때 검정을 중지하려고 노력함으로써 실험을 실행하기 전에 대답해야 합니다. 실험 기간의 베이스라인을 결정하기위해, 흔한 접근은 다음의 공식을 사용하는 것입니다 :

예를 들어, 이 공식으로 14 가 계산되었다면, 이것은 2주동안 테스트 되어야 한다는 것을 의마합니다. 그러나 테스트를 실행하는 시간과 시간을 결정할 때 여러 가지 비즈니스별 요소를 고려하고 이 공식을 어느 정도 과장하여 사용하는 것이 매우 중요합니다.

예를 들어, COVID-19 팬데믹이 전 세계를 뒤흔든 2020년 1월 초에 실험을 실행하고 이것이 페이지 사용량에 영향을 미쳤다면, 일부 기업의 경우 이는 페이지 사용량의 높은 증가를 의미하며, 일부 기업의 경우 이를 고려하지 않고 A/B 테스트를 실행한 후 사용성이 크게 감소하면 활동 기간이 일반적인 페이지 사용량의 진정한 표현이 아니기 때문에 부정확한 결과를 초래할 수 있습니다.

너무 짧은 테스트 기간 : Novelty Effects (참신성효과)

사용자들은 그들의 특성과 무관하게 모든 유형의 변화를 빠르고 긍정적으로 반응하는 경향이있습니다. 이 실험 군에 대한 긍정적인 효과는 전체적으로 변화가 무엣인지와는 무관하게 변화이기 때문에 발생하는 것으로 novelty effect (참신성 효과) 라고 언급됩니다. 그리고 시간이 지나면 사라지기 때문에 "illusory (착각을 일으키는 (?)) " 것으로 간주됩니다. 그래서, 실험군 그 자체로 효과가 있다고 묘사하는 것은 잘못되었으며, 계속해서 참신성 효과가 사라질 때 까지 기다려야합니다.

그래서, 우리가 필요한 테스트 기간을 고를 때, 확실히 하기 위해서 너무 짧은 기간은 수행하지 마세요. 그렇지 않으면 참신성 효과를 가지게 됩니다. 참신성 효과는 A/B 테스트의 외부적 유효성에 대한 주된 위협이 될 수 있습니다. 그래서 가능한 피하는 것이 중요합니다.

너무 긴 테스트 기간 : Maturation Effects (만기 효과)

A/B 테스트를 계획할 때 모든 사용자들이 새로운 기능과 제품에 대해 인지할 때까지 충분한 테스트 기간을 고려하는것이 좋습니다. 이와 같이 처치의 일환으로 도입된 변화로 인해 초기의 긍정적 반응이나 관심 급증으로부터 냉각될 수 있도록 복귀 사용자에게 더 많은 시간을 주어 실제 치료 효과를 관찰할 수 있을 것입니다. 이는 참신성 효과를 피하고 테스트 결과에 더 좋은 예측치를 얻는데 도움이 됩니다. 그러나 테스트 기간이 길수록 외부 효과가 사용자의 반응에 영향을 미치고 테스트 결과를 오염시킬 가능성이 있습니다. 이것이 Maturation Effects (만기 효과)입니다. 그래서, A/B 테스트를 너무 오랫동안 수행하는 것도 또한 추천하지 않고 결과의 신뢰성을 증가하기 위해 피하는 것이 좋습니다.

테스트 기간이 길어질 수록, 외부 효과가 사용자의 반응에 영향을 미치고 테스트 결과를 오염시킬 가능성이 있습니다.

Step 5: Running the A/B test (A/B 테스트 수행)

준비가 끝나면, 엔지니어링의 도움으로 A/B 테스트를 수행할 수 있습니다. 첫번째로, 엔지니어링 팀은 통제군과 실험군의 무결성이 지켜지도록 보증해줄 필요가 있습니다. 두번째로, 처치에 대한 사용자의 반응을 저장하는 메커니즘은 체계적인 편향을 피하기 위해 모든 사용자들에게 정확하고 동일하게 적용되어야 합니다. 또한 검정을 시작하기 전에 계산된 최소 표본 크기에 도달하지 않은 상태에서 통계적 유의성 (작은 p-값)을 감지하여 검정을 너무 일찍 중지하는 것과 같은 작업은 하지 않는 것이 좋습니다.

Step 6: Analyzing A/B test results with Python (A/B 테스트 결과 분석)

A/B 테스트의 결과를 해석할 때, 이전에 언급된 통계적 가설 검정하기 위해 계산해야하는 일련의 값들이 있습니다. 통제 집단과 실험 집단 간에 통계적으로 유의미한 차이가 있는지 검정하기 위해 필요한 값들은 아래 것들을 포함합니다 :

적절한 통계 기법 선택
통계량 계산 (T)
통계량의 p-value 계산
통계적 가설 기각 또는 기각할 수 없음 (통계적 유의성)
오차 한계 계산 ( 그 실험의 외적 타당성)
신뢰 구간 계산 ( 외적 타당성과 실험의 실용적 유의성)

Choosing an appropriate statistical test

한번 통제군과 실험군의 상호작용 데이터가 수집이되면, 모수적 그리고 비모수적 방법으로 분류된 통계적 기법들 중 적절한 것을 선택하여 이전의 통계적 가설 검정을 수행할 수 있습니다. 기법의 선택은 다음 요인에 의해 결정됩니다 :

주요 지표의 형태 (underlying pdf)
표본 크기 (for CLT)
통계적 가설의 특성 (두 그룹간의 관계가 있음을 보여주거나, 두 그룹간 관계의 유형을 식별함)

A/B 테스트에서 사용되는 가장 유명한 모수적 기법은 다음과 같습니다.

2-Sample T-test ( N<30 일 때, 지표는 student-t 분포를 따릅니다. 그리고 통제 집단과 실험 집단 간의 관계의 유형과 관계까 있는지 식별하고자 할 때 사용합니다. )
2-Sample Z-test ( N>30 일때, 지표는 근사적 정규 분포를 따릅니다. 그리고 실험군과 통제 집단 간의 관계 유형과 관계가 있는지 식별하고자 할 때 사용합니다. )

A/B 테스트에서 사용되는 가장 유명한 비-모수적 기법은 다음과 같습니다.

Fisher Exact test ( 작은 N 일때, 통제군과 실험군 간의 관계가 존지하는지 식별하고자 할 때 사용됩니다)
Chi-Square test ( 큰 N일 때, 통제군과 실험군 간의 관계가 존재하는지 식별하고 자 할 때 사용됩니다)
Wilcoxon Rank Sum/Mann Whitney test ( 작은 N이거나 큰 N일 때, 치우친 표본 분포일 때, 통제군과 실험군의 중앙값에 차이가 있는지 검정합니다)

2-sample T-test

만약, 대조군과 실험군의 재표가 평균과 같은 형태 (예를 들어, 평균 구매량) 에서 통계적으료 유의미한 차이가 있는지 검증하길 원한다면 , 지표는 표본 크기가 30보다 작을 때 student-t 분포를 따르기 때문에 다음의 가설을 T-test로 검정해볼 수 있습니다.

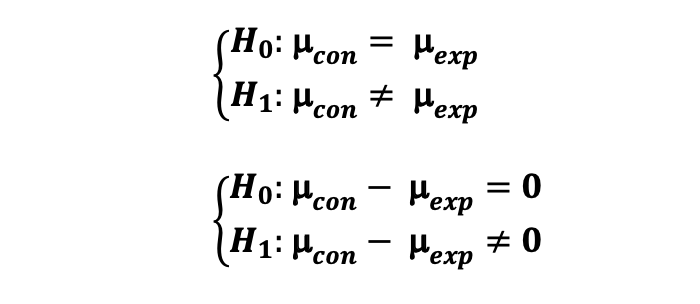
여기서 대조군의 표본 평균의 분포는 자유도가 N_con -1 인 Student-t 분포를 따릅니다. 실험군의 표본 평균의 분포 또한 자유도가 N_exp - 1 인 Student-t 분포를 따릅니다. N_con 과 N__exp 가 대조군과 실험군의 사용자 수라는 것이라는 것을 기억하세요.

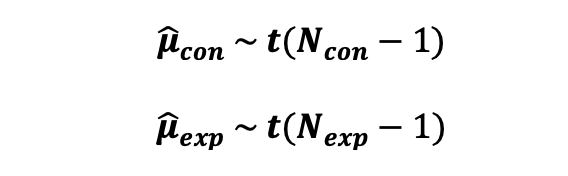
그리고, 두 표본의 집단의 분산을 추정하기위해 다음과 같이 계산합니다.

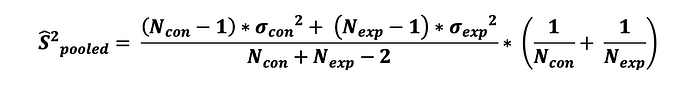
여기서 $\sigma^2_{con}$ 과 $\sigma^2_{exp}$ 는 통제군과 실험군의 표본 분산을 의미합니다. 그리고 표본 오차는 추정된 집단의 분산에 루트를 씌운것과 동일하며 다음과 같이 정의됩니다.

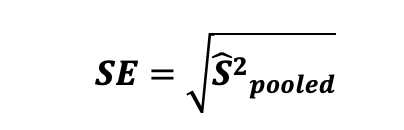
그에 따라서, 아까 언급한 가설에 대한 2-sample T-test의 통계량은 다음과 같이 계산됩니다.

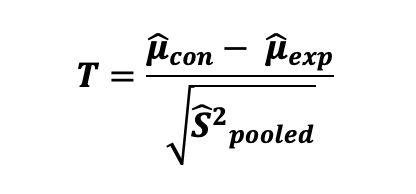
관찰된 두 표본 평균 사이의 통계적 유의성을 검정하기 위해, 우리의 통계량에 대한 p-value를 계산할 필요가 있습니다. p-value는 임의의 확률로 인한 것일 때 적어도 공통 값만큼은 극단적인 값을 관측할 확률입니다. 다르게 말하면, p-value는 귀무 가설이 참이라고 가정할 때 표본 데이터의 효과만큼 극단적인 효과를 얻을 확률입니다. 그러면, 통계량의 p-value는 다음과 같이 계산됩니다:

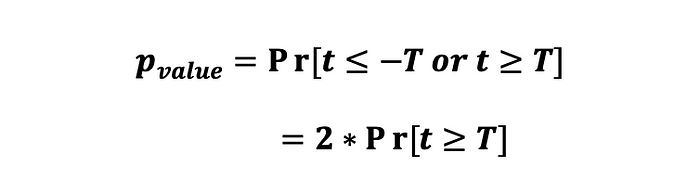
p-value의 해석은 검정력 분석을 통해 검정을 수행하기 전에 선택한 유의 수준 alpha에 따라 결정됩니다. 만약 계산된 p-value가 0.05보다 작거나 같게 나타난다면 (예를들어 5% 신뢰수준인 0.05 ) 우리는 귀무가설을 기각하고 통제군과 실험군의 주요 지표 간에 통계적으로 유의미한 차이가 있다는 것을 증명할 수 있습니다.

마지막으로, 얻은 결과가 얼마나 정확한지 결정하고 얻은 결과의 실용적인 유의성에 대해 말하자면, 다음 공식을 사용해서 검정에 대한 신뢰구간을 계산할 수 있습니다.

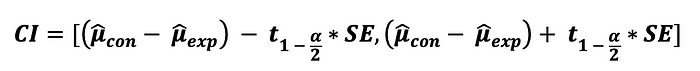
여기서, $t_{1-alpha/2}$ 는 신뢰 수준인 alpha와 t-table에서 확인할 수 있는 양 끝의 t-test에 상응하는 critical value 입니다.

import numpy as np
from scipy.stats import t

N_con = 20
df_con = N_con - 1 # degrees of freedom of Control 
N_exp = 20
df_exp = N_exp - 1 # degrees of freedom of Experimental 

# Significance level
alpha = 0.05

# data of control group with t-distribution
X_con = np.random.standard_t(df_con,N_con)
# data of experimental group with t-distribution
X_exp = np.random.standard_t(df_exp,N_exp)

# mean of control
mu_con = np.mean(X_con)
# mean of experimental
mu_exp = np.mean(X_exp)

# variance of control
sigma_sqr_con = np.var(X_con)
#variance of control
sigma_sqr_exp = np.var(X_exp)

# pooled variance
pooled_variance_t_test = ((N_con-1)*sigma_sqr_con + (N_exp -1) * sigma_sqr_exp)/(N_con + N_exp-2)*(1/N_con + 1/N_exp)

# Standard Error
SE = np.sqrt(pooled_variance_t_test)

# Test Statistics
T = (mu_con-mu_exp)/SE

# Critical value for two sided 2 sample t-test
t_crit = t.ppf(1-alpha/2, N_con + N_exp - 2)

# P-value of the two sided T-test using t-distribution and its symmetric property
p_value = t.sf(T, N_con + N_exp - 2)*2

# Margin of Error
margin_error = t_crit * SE
# Confidence Interval
CI = [(mu_con-mu_exp) - margin_error, (mu_con-mu_exp) + margin_error]

print("T-score: ", T)
print("T-critical: ", t_crit)
print("P_value: ", p_value)
print("Confidence Interval of 2 sample Z-test: ", np.round(CI,2))

https://m.blog.naver.com/sendmethere/221333164258?view=img_9

[통계교육] 풀어쓰는 통계 - t 검정(t-test)이란?

1. t 검정을 비롯한 관련 용어 설명 2. t 검정의 특징 t검정의 특징을 정리하자면 다음과 같다. 3. t...

blog.naver.com

2-sample Z-test

만약, 통제군과 실험군의 지표가 평균의 형태 (예를 들어, 평균 구매량) 또는 비율의 형태 (예를들어 클릭률)과 같은 지표이면서 정규 분포를 따르거나 표본 크기가 30보다 큰 경우에 중심 극한 정리에 따라 표본 분포가 정규 분포에 근사한다고 할 수 있는 경우에, 통계적으로 유의미한 차이가 있는지 검정하고자 한다면 2-sample Z-test를 사용할 수 있습니다. 여기서 두가지 케이스에 대해 구분을 짓겠습니다. 한가지 케이스는 주요 지표가 비율의 형태 (예를 들어 클릭률) 이고, 또 다른 한가지는 주요 지표가 평균의 형태 (예를 들어 구매량 평균)입니다.

Case 1: Z-test for comparing proportions (2-sided)
만약, 통제군과 실험군의 지표가 비율 (예를 들어, CTR)의 형태이고, 클릭 이벤트가 독립적으로 일어날 때, 두 지표간 통계적으로 유의미한 차이가 있는지 검정하고자 할 때, 다음과 같은 가설에 따라 2-sample Z-test를 해볼 수 있습니다 :

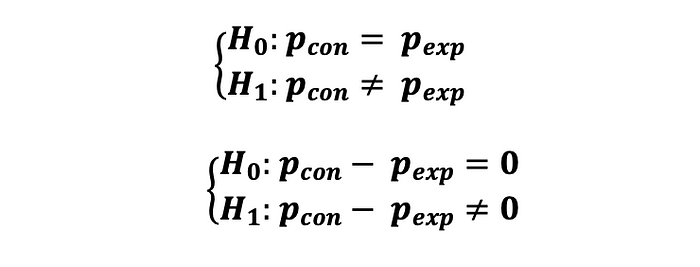
여기서 각 클릭 이벤트는 p_con 및 p_exp와 함께 베르누이 분포(클릭: 성공 및 없음: 실패)를 따르는 두 가지 가능한 값 1(성공) 및 0(실패)을 취할 수 있는 확률 변수로 설명할 수 있다. 즉 :

여기서, 통제군과 실험군 사용자의 상호작용 데이터를 수집한 후에, 다음과 같은 두 확률 추정치를 계산할 수 있다.

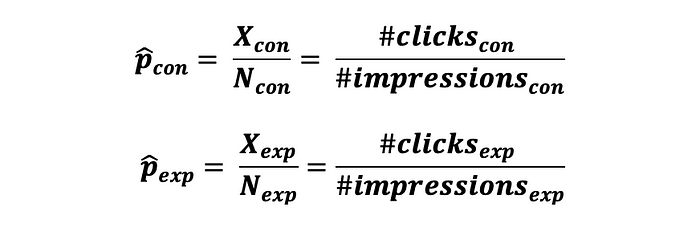
이 확률간 차이를 테스트할 때, 성공 확률의 집합 추정치와 집합 분산을 구할 필요가 있으며 다음과 같이 계산할 수 있다.

다음 표본 오차는 집합 분산 추정치에 루트를 씌운값과 동일하며 다음과 같이 계산될 수 있다:

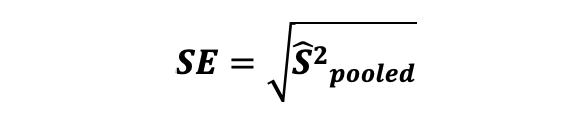
그에 따라, 비율 차이에 대한 2-sample Z-test 의 테스트 통계량은 다음과 같이 계산될 수 있다.

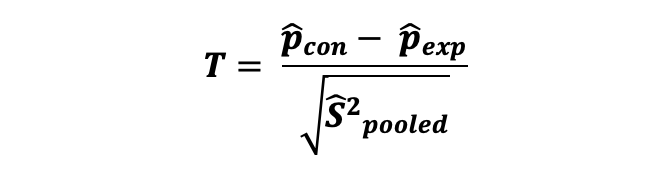
그리고, 통계량에 대한 p-value는 다음과 같이 계산될 수 있다.

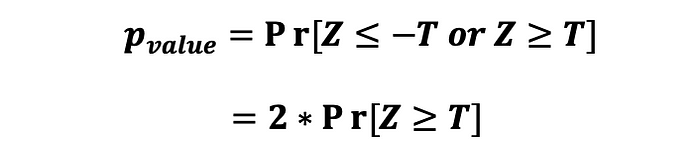
마지막으로, 통계량의 신뢰구간은 다음과 같이 계산할 수 있다 :

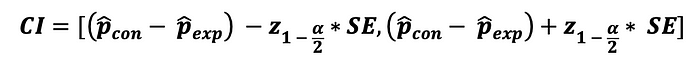
여기서 $z_{1-alpha/2}$ 는 신뢰 수준 alpha에 대한 양 끝 Z-test에 상응하는 통계량의 critical value 이며, Z-table 에서 찾을 수 있다. 2-sample Z-test의 기각역은 다음 그래프로 표현될 수 있다.

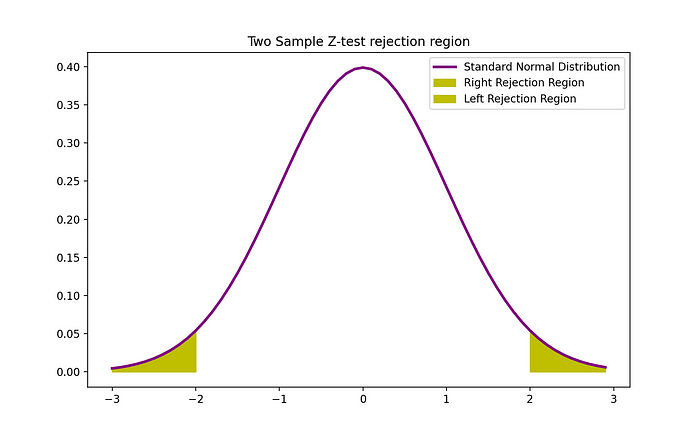
import numpy as np
from scipy.stats import norm

X_con = 1242 #clicks control
N_con = 9886 #impressions control
X_exp = 974 #clicks experimental
N_exp = 10072 #impressions experimetal

# Significance Level
alpha = 0.05

p_con_hat = X_con / N_con
p_exp_hat = X_exp / N_exp

p_pooled_hat = (X_con + X_exp)/(N_con + N_exp)
pooled_variance = p_pooled_hat*(1-p_pooled_hat) * (1/N_con + 1/N_exp)

# Standard Error
SE = np.sqrt(pooled_variance)

# test statsitics
Test_stat = (p_con_hat - p_exp_hat)/SE
# critical value usig the standard normal distribution
Z_crit = norm.ppf(1-alpha/2)

# Margin of error
m = SE * Z_crit
# two sided test and using symmetry property of Normal distibution so we multiple with 2
p_value = norm.sf(Test_stat)*2

# Confidence Interval
CI = [(p_con_hat-p_exp_hat) - SE * Z_crit, (p_con_hat-p_exp_hat) + SE * Z_crit]

if np.abs(Test_stat) >= Z_crit:
    print("reject the null")
    print(p_value)

print("Test Statistics stat: ", Test_stat)
print("Z-critical: ", Z_crit)
print("P_value: ", p_value)
print("Confidence Interval of 2 sample Z-test for proportions: ", np.round(CI,2))

import matplotlib.pyplot as plt
z = np.arange(-3,3,  0.1)
plt.plot(z, norm.pdf(z), label = 'Standard Normal Distribution',color = 'purple',linewidth = 2.5)
plt.fill_between(z[z>Z_crit], norm.pdf(z[z>Z_crit]), label = 'Right Rejection Region',color ='y' )
plt.fill_between(z[z<(-1)*Z_crit], norm.pdf(z[z<(-1)*Z_crit]), label = 'Left Rejection Region',color ='y' )
plt.title("Two Sample Z-test rejection region")
plt.legend()
plt.show()

https://math100.tistory.com/91

두 모비율 차이의 가설검정하는 법

이전 글에서 다루었던 “두 모평균”과 마찬가지로, 두 모비율의 가설검정도 집단 각각의 모수를 파악하는 것이 아니라, 두 집단의 모비율이 서로 어떠한 관계에 있는지를 파악하는 것이다. 그

math100.tistory.com

https://math100.tistory.com/92?category=836925

두 모비율 차이의 가설검정 문제풀이

단일 모비율의 가설검정과 마찬가지로, 두 모비율의 가설검정은 검정통계량을 구하는 공식이 신뢰구간과 다르므로 조심해야 한다. 그리고 모비율의 가설검정은 기본적으로 정규분포를 사용하

math100.tistory.com

Case 2: Z-test for comparing means (2-sided)

만약, 통제군과 실험군의 지표가 평균의 형태일 때 (예를 들어, 일별 CTR) 통계적으로 유의한 차이가 있는지 검정하고자 한다면, 2-sample Z-test를 아래의 가설에 따라 수행해볼 수 있다:

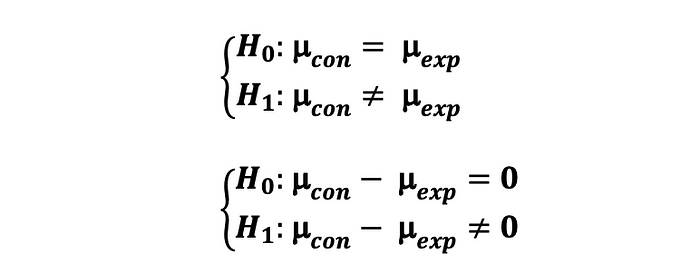
여기서 통제군의 표본 평균의 분포는 평균이 $\mu_{con}$ 분산이 $\sigma^2_{con} / N_{con} $ 을 따른다. 게다가 실험군의 표본 평균의 분포도 평균이 $\mu_{exp}$ 분산이 $\sigma^2_{exp} / N_{exp} $ 를 따른다.

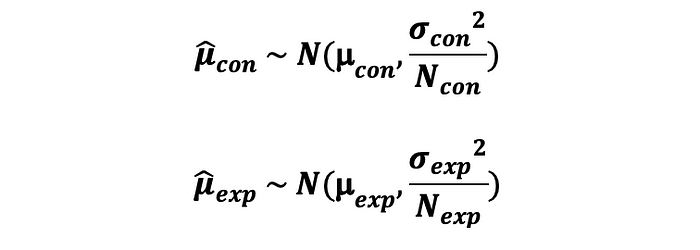
그러면, 통제군과 실험군의 평균에 차이 또한 평균이 $\mu_{con} - \mu_{exp}$ 분산이 $\sigma^2_{con} / N_{con} + \sigma^2_{exp} / N_{exp} $ 를 따른다.

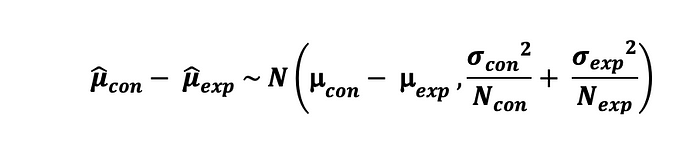
그에 따라, 차이에 대한 2-sample Z-test 의 통계량은 다음과 같이 계산된다.

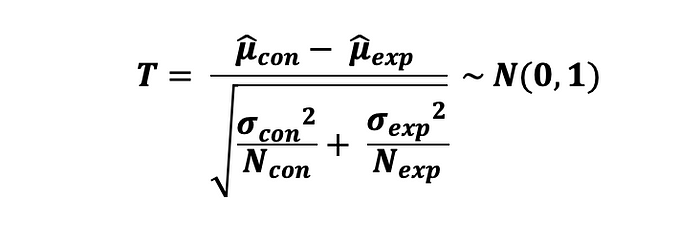
표본 오차는 추정된 분산의 추정치에 루트를 씌운 것과 같으며 다음과 같이 정의된다 :

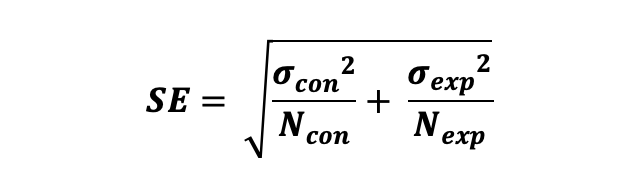
그리고 나서, 통계량의 p-value는 다음과 같이 계산된다.

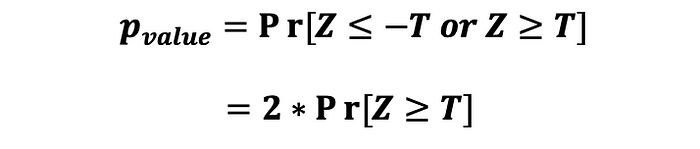
마지막으로, 통계량의 신뢰구간도 다음과 같이 계산할 수 있다 :

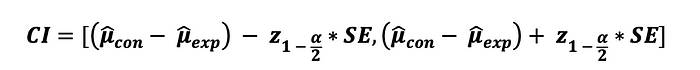
import numpy as np
from scipy.stats import norm

N_con = 60
N_exp = 60

# Significance Level
alpha = 0.05

X_A = np.random.randint(100, size = N_con)
X_B = np.random.randint(100, size = N_exp)

# Calculating means of control and experimental groups
mu_con = np.mean(X_A)
mu_exp = np.mean(X_B)

variance_con = np.var(X_A)
variance_exp = np.var(X_B)

# Pooled Variance
pooled_variance = np.sqrt(variance_con/N_con + variance_exp/N_exp)

# Test statistics
T = (mu_con-mu_exp)/np.sqrt(variance_con/N_con + variance_exp/N_exp)

# two sided test and using symmetry property of Normal distibution so we multiple with 2
p_value = norm.sf(T)*2

# Z-critical value
Z_crit  = norm.ppf(1-alpha/2)

# Margin of error
m = Z_crit*pooled_variance

# Confidence Interval
CI = [(mu_con - mu_exp) - m, (mu_con - mu_exp) + m]


print("Test Statistics stat: ", T)
print("Z-critical: ", Z_crit)
print("P_value: ", p_value)
print("Confidence Interval of 2 sample Z-test for proportions: ", np.round(CI,2))

import matplotlib.pyplot as plt
z = np.arange(-3,3,  0.1)
plt.plot(z, norm.pdf(z), label = 'Standard Normal Distribution',color = 'purple',linewidth = 2.5)
plt.fill_between(z[z>Z_crit], norm.pdf(z[z>Z_crit]), label = 'Right Rejection Region',color ='y' )
plt.fill_between(z[z<(-1)*Z_crit], norm.pdf(z[z<(-1)*Z_crit]), label = 'Left Rejection Region',color ='y' )
plt.title("Two Sample Z-test rejection region")
plt.legend()
plt.show()

Chi-Squared test

만약, 통제군과 실험군의 성증 지표 (예를 들어 전환율) 간에 통계적으로 유의미한 차이가 있는지를 검증하고자 한다면 그리고 어떤것이 더 좋은지 이 관계 자체에 대해서는 알 필요가 없다면 (단측 검정 불가) 다음과 같은 가설로 Chi-Square test 를 수행해볼 수 있다.

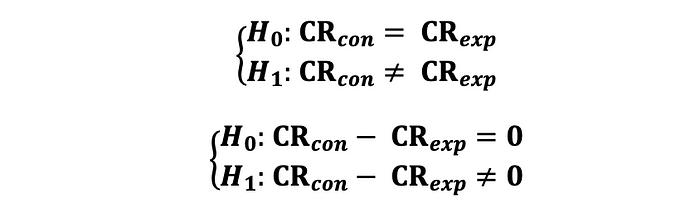
이 지표는 이항 변수 (예를들어 전환 또는 미전환/ 클릭 또는 미클릭) 과 같은 이항 변수의 형태일때 가능하다는 점을 명심하세요. 이 데이터는 다음 테이블의 형태로 나타낼수 있는데, O와 T는 각각 관측치와 이론치(이론상 값) 를 뜻합니다.

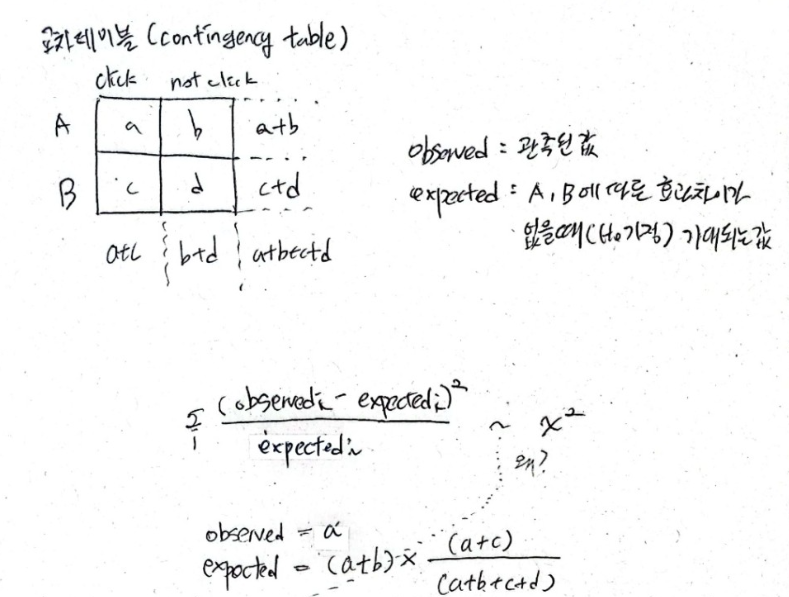
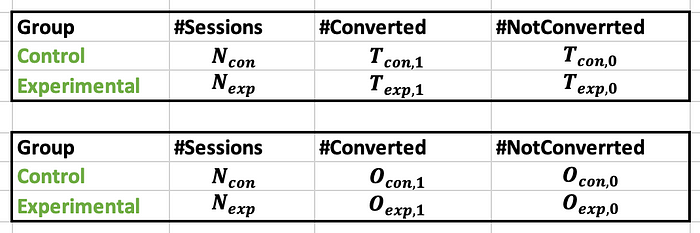
https://blog.naver.com/plasticcode/222620878854

여기서 Chi-2 test에 따라 통계량은 다음과 같이 계산됩니다 :

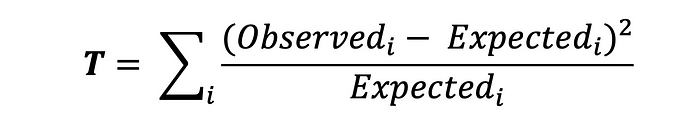
여기서 Observed는 관찰된 데이터를 의미하며 Expected는 이론적 값을 의미합니다. 그리고 i 는 0(미 전환) 과 1 (전환) 의 값을 가질 수 있습니다. 이 요소들은 각각 다른 분모를 가지고 있다는 것을 확인하는 것이 중요합니다. 두 개의 그룹만 있는 경우 검정 통계량에 대한 공식은 다음과 같이 나타낼 수 있습니다:

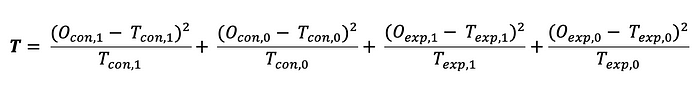
기대값은 단순히 제품의 각 버전을 보는 횟수에 전환(또는 CTR의 경우 클릭)으로 이어질 확률을 곱한 것과 같다.

Chi-2 검정은 모수적 테스트가 아니라는 것을 명심하세요. 이것의 표본오차와 신뢰구간은 Z-test나 T-test의 모수적 방식으로 수행했던 일반적인 방식으로는 계산될수 없습니다.

이 양면 2-smaple Z-검정의 기각 영역은 다음 그래프로 시각화할 수 있다.

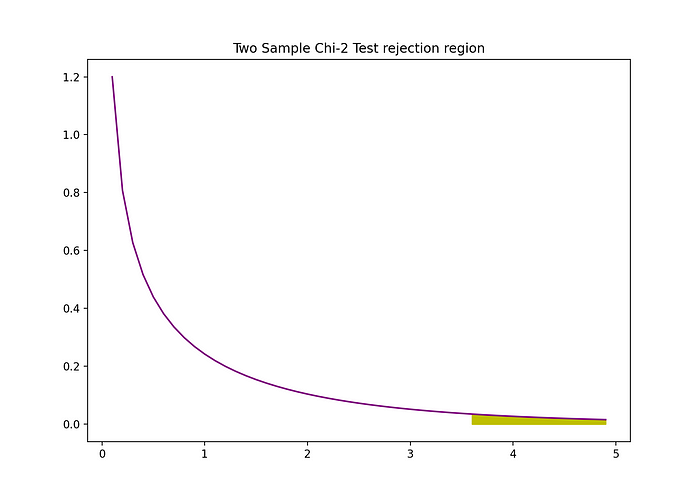
import numpy as np
from scipy.stats import chi2

O = np.array([86, 83, 5810,3920])
T = np.array([105,65,5781, 3841])

# Squared_relative_distance

def calculate_D(O,T):
    D_sum = 0
    for i in range(len(O)):
        D_sum += (O[i] - T[i])**2/T[i]
    return(D_sum)

D = calculate_D(O,T)
p_value = chi2.sf(D, df = 1)


import matplotlib.pyplot as plt
# Step 1: pick a x-axis range like in case of z-test (-3,3,0.1)
d = np.arange(0,5,0.1)
# Step 2: drawing the initial pdf of chi-2 with df = 1 and x-axis d range we just created
plt.plot(d, chi2.pdf(d, df = 1), color = "purple")
# Step 3: filling in the rejection region
plt.fill_between(d[d>D], chi2.pdf(d[d>D], df = 1), color = "y")
# Step 4: adding title
plt.title("Two Sample Chi-2 Test rejection region")
# Step 5: showing the plt graph
plt.show()

구매여부 데이터 AB 테스트 python 코드 예시

data = pd.read_csv('ABtest_sample.csv')
data.head(10)

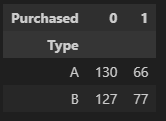
crosstab_df = pd.crosstab(index = data['Type'], columns = data['Purchased'])
crosstab_df

from scipy.stats import chi2


def get_chi2_test_statistics(crosstab:pd.DataFrame): 

    result = crosstab.to_numpy()
    
    x_sum = result.sum(axis = 0)
    y_sum = result.sum(axis = 1)
    tot_sum = result.sum()

    e = [x_sum[i] * y_sum[j] / tot_sum for i in range(0,2) for j in range(0,2)]
    o = [result[i,j] for i in range(0,2) for j in range(0,2)]
    return e, o 

def calculate_D(O, E):
    D_sum = 0
    for i in range(len(O)):
        D_sum += (O[i] - E[i]) **2 / E[i]
    return (D_sum)

alpha = 0.05 
e, o = get_chi2_test_statistics(crosstab_df)
D = calculate_D(o, e)

p_value = chi2.sf(D, df = 1)
print(round(p_value, 2))

if p_value < alpha:
    print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
    print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
    
>> 0.0
Reject the null hypothesis. There is a significant difference between the groups.

비모수 검정의 표준오차와 신뢰구간

모수 검정 케이스에서 표준오차와 신뢰 구간 계산은 간단하다. 하지만, 비모수 검정에서는 간단하지 않다. 대조군과 실험군의 표본 평균 또는 표본 중앙값을 비교하기 위한 목적으로 비모수 통계 검정에서 표준 오차와 신뢰구간을 계산하기 위해, 부트스트래핑 과 부트스트랩 사분위수 방법 과 같은 재표본추출 기법을 사용할 필요가 있다.

부트스트랩이 하는 일은 원래 훈련 샘플을 가져다가 교체하여 다시 샘플링하여 B개의 다른 샘플이 생성된다는 것이다. 따라서 부트스트랩의 아이디어는 두 그룹의 기존 데이터, 실험 중에 수집된 데이터, 즉 B번에서 교체하여 다시 샘플링하는 것이다(부트스트랩 데이터 세트에서 동일한 관찰이 두 번 이상 발생할 수 있음). 그런 다음 다음 다음 Bx1 벡터로 표시할 수 있는 대조군 및 실험군 B의 표본 평균/중앙값을 계산해야 합니다:

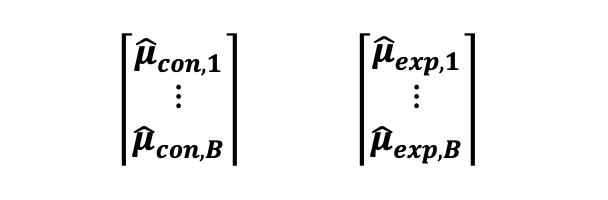
결과적으로, B 샘플로부터 평균 차이로 도출한 대조군과 실험군 쌍의 표본 평균의 차이를 계산할 수 있게 됩니다. 아 차이의 표본 푼포를 표본 평균으로 그릴 수도 있으며, 이 분포는 다음 Bx1 벡터로 나타낼 수 있습니다 :

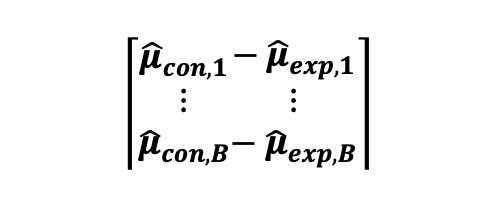
그리고 나서, B가 큰 수라면 ( 예시로 B = 1000) , 우리는 중심 극한 정리에 의하여 대조군과 실험군 평균의 차이에 대한 표본 분포가 정규 분포를 따른다고 가정할 수 있고, 아래의 그림처럼 보일 수 있습니다.

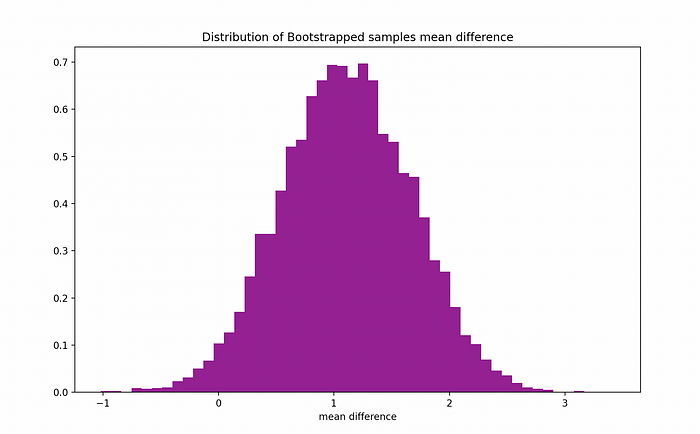
그리고 나서, 이 검정의 p-값을 구하기 위해 평균의 차이가 0보다 크므로 B의 횟수를 계산해야 합니다:

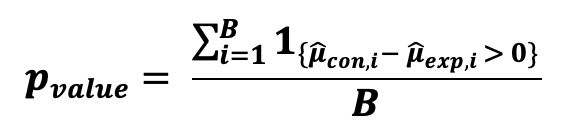
만약 p-value가 선택한 신뢰 수준보다 크다면, 귀무가설을 기각 할수 없다고 주장할 수 있습니다. 그래서 대조군과 실험군 의 표본 평균의 차이에 통계적으로 유의미한 차이가 있다고 주장할 충분한 증거가 없다고 할수 있습니다. Bootstrapping은 표본 중앙값에 대해서도 동일하게 수행될 수 있습니다.

95% 신뢰 구간을 계산하기 위해서는 추정치의 부트스트랩 분포의 2.5번째와 97.5번째 백분위수를 구간의 하한과 상한으로 사용하는 백분위수법을 사용할 수 있습니다.

import numpy as np
import pandas as pd
from scipy.stats import norm

N = 100
X = pd.Series(np.random.binomial(300,0.7,size =N))
Y1 = np.repeat("Exp",N/2)
N_exp = len(Y1)
Y2 = np.repeat("Cont",N/2)
N_con = len(Y2)

Y = pd.Series(np.append(Y1,Y2))
data = pd.concat([X,Y],axis = 1)
print(data)
means_per_group = data.groupby(1, group_keys = False)[0].mean()
medians_per_group = data.groupby(1)[0].median()

alpha = 0.05
def Bootrapping_for_diff_means_medians(data,B):
    boot_mean_diff = []
    boot_medians_diff = []

    boot_means_con = []
    boot_means_exp = []

    count_num_positives_meandiff = 0
    count_num_positives_mediandiff = 0

    for i in range(B):

        boot_sample = data.sample(frac = 1, replace = True)

        #means of bootstrap sample for control and experimental group
        boot_means_per_group = boot_sample.groupby(1)[0].mean()
        boot_sample_mean_con = boot_means_per_group["Cont"]
        boot_sample_mean_exp = boot_means_per_group["Exp"]

        boot_means_con.append(boot_sample_mean_con)
        boot_means_exp.append(boot_sample_mean_exp)

        # calculating the difference in means per bootstrap sample
        diff_means = boot_sample_mean_exp - boot_sample_mean_con

        #counting number of times is the difference positive
        if diff_means > 0:
            count_num_positives_meandiff += 1

        # medians of bootstrap sample for control and experimental group
        boot_medians_per_group = boot_sample.groupby(1)[0].median()

        # calculating the difference in medians per bootstrap sample
        diff_medians = boot_medians_per_group["Exp"] - boot_medians_per_group["Cont"]
        if diff_medians > 0:
            count_num_positives_mediandiff += 1

        boot_mean_diff.append(diff_means)
        boot_medians_diff.append(diff_medians)

    return(boot_means_con,boot_means_exp,count_num_positives_meandiff,count_num_positives_mediandiff,boot_mean_diff)

B = 10000
X_bars_con,X_bars_exp ,n_means, n_medians,boot_mean_diff = Bootrapping_for_diff_means_medians(data,B)
**Z_mean = np.mean(X_bars_exp)- np.mean(X_bars_con)
Z_sigma = np.sqrt((np.var(X_bars_exp)/N_exp + np.var(X_bars_con)/N_con))
CI = [Z_mean - norm.ppf(1-alpha/2)*Z_sigma, Z_mean + norm.ppf(1-alpha/2)*Z_sigma]**

print("Mean of X_bar_exp - X_bar_con", Z_mean)
print("Standard Error of X_bar_exp - X_bar_con", Z_sigma)
print("CI of X_bar_exp - X_bar_con", CI)

p_value_diff_means = n_means/B
p_value_diff_medians = n_medians/B

CI = np.percentile(boot_mean_diff, [2.5, 97.5])

import matplotlib.pyplot as plt
counts,bins,ignored = plt.hist(boot_mean_diff,50,density = True,color = 'purple')
plt.xlabel("mean difference")
plt.title("Distribution of Bootstrapped samples mean difference")
plt.show()

p-value가 선택한 신뢰 수준 보다 더 크다면, 우리는 귀무가설을 기각할 수 없다고 주장할 수 있습니다. 그에 따라 대조군과 실험군의 표본 평균에 통계적으로 유의미한 차이가 있다고 주장할 만한 충분한 증거가 있다고 할 수 없습니다.

통계적 유의성 vs 실용적 유의성

A/B 테스팅의 통계적 측면에서, 작은 p-value가 검출이 되면, 통계적 유의성에 대해 말할 수 있습니다. 하지만 통계적 유의성 만으로는 피쳐나 제품의 출시를 추천하기에 충분하지 않습니다.

통계적 유의성이 탐지된 이후에, 다음 단계로 실용적 유의성 이 있는지를 이해하는 것입니다. 이를 통해 두 그룹의 성과 차이가 감지된 것이 투자를 정당화할 만큼 큰지, 아니면 너무 작아서 출시 결정을 내리는 것이 투자 가치가 없는지 이해하는 데 도움이 될 것입니다.

A/B 테스트가 실용적 유의성이 있는지 결정하는 한가지 방법으로는 신뢰구간을 사용하여 MDE (경제적 유의성 추정치)의 하한과 비교해보는 것입니다. 좀 더 구체적으로, 만약 CI의 하한이 MDE (델타) 보다 더 크다면, 실용적 유의성이 있다고 말할 수 있습니다. 예를 들어 만약 CI = [5%, 7.5%] 이고, MDE가 3% 라면, 5% > 3% 이기 때문에 실용적 유의성이 있다고 결론을 지을 수 있습니다.

CI의 넓이를 잘 살펴보고 너무나 크진 않는지 확실히 해야합니다. 왜냐하면 너무 넓은 CI는 당신의 결론에 대한 정확도가 낮으며 이 결과가 전체 모수에 대하여 일반화되지 않았다고 암시할 수 있기 때문입니다. (외부적 유효성)

A/B Test 품질

A/B 테스팅은 실험 설계의 한 예로, 다른 종류의 실험들 처럼, 견고한 결론과 제품에 대한 의사결정을 내리기 위해 만족해야할 3가지 요인들이 있습니다. 이 요소들은 다음과 같습니다.

신뢰성(Reliability) /복제성(Replicability)
타당성(Validity)
유효성(Potency)

신뢰성(Reliability) and 복제성(Replicability)

신뢰성의 이면에 있는 아이디어는 실험 결과가 일회성 발견 이상이어야 하며 본질적으로 재현 가능하고 반복 가능해야 한다는 것입니다. 최근 연구자들이 실험 결과를 재생산 하기 어렵기 때문에, 재현가능성의 위기 라는 현상이 연구계에 나타났고습니다. 이것은 다음과 같은 다른 이유들 때문에 발생할 수 있습니다. :

원래의 시험이 변경되었거나 p-hacking이 있을 때
원래 실험에서의 측정 오류가 있을 때
원래 실험에서의 체계적 오류가 있을 때
실험을 수행할 때 사용된 소스코드나 데이터의 문서화가 부족할 때

아래의 것들로 당신의 A/B 테스트 실험의 신뢰성을 향상시킬 수 있습니다.

안전한 클라우드에 코멘트와 함께 소스코드를 저장하세요.
안전한 클라우드에 코멘트와 함께 데이터를 저장하세요
과정과 결과에 대한 상세한 문서화를 수행하세요
체계적 오류를 확인하세요. (처치 반응이 보고되는 방식으로, 처치에 대한 영향력을 어떻게 측정했는지)
다른 도시에서 같은 분석을 수행해보세요
샘플링 기법이나 시뮬레이션으로 랜덤시드를 사용해 보세요.

모든 단계에서 당신의 작업을 더욱 신뢰성 있게 만들어 줄 것입니다.

타당성(Validity)

타당성은 실험의 전체 개념을 포괄하며, 얻은 결과가 무작위 대조군 실험의 모든 요구 사항을 충족하는지 여부를 결정합니다. 타당성의 경우, 보통 두가지 유형의 Validity로 구분합니다.

내부적 타당성
외부적 타당성

내부적 타당성은 관찰된 데이터와 이로 부터 얻은 결과를 의미합니다. 모둔 결과들이 유효하고 신뢰성이 있나요? 부정확 하거나 비편향적이진 않나요? 종속변수의 변화는 개입(독립변수)에 의한 것일 뿐 다른 요인에 의한 것이 아닌가요? 당신의 A/B 테스트 실험에 부정적으로 영향을 줄 수 있는 문제들의 예는 다음과 같다.

생략된 변수 편향 (Heckman 2 Step Process 를 사용하세요)
역 인과 관계(IV 또는 2SLS 접근 방식을 사용하세요)
가짜 변수(목표 변수에 대한 통제 변수 또는 도구(instrument) 를 찾아보세요)
부적절한 대리변수 사용 (실제 개입 변수를 사용하세요)

외부적 타당성은 당신의 실험 결과가 전체 모수에 일반화 될 수 있는 정도를 의미합니다. 이것은 다음 질문에 대답을 하게 됩니다: 이 결과가 더 넓은 사람들에게 일반화되어 적용될 수 있을까? 외부적 유효성은 같은 조건 하에 실험을 반복하는 실험을 반복함으로써 외부적 유효성은 향상될 수 있을까요? A/B 테스트 실험의 외부적 유효성에 부정적으로 영향을 줄 수 있는 문제들의 예는 다음과 같습니다.

편향된 샘플 (비편향된 샘플을 임의로 추출하기 위해 solid 샘플링 기법을 사용하세요. )
대표성이 없는 표본 ( 비편향되었을 뿐만아니라 당신의 모수에 대표적인 샘플을 만들어 내기 위해 가중 또는 층화 추출 과 같은 고급 통계적 샘플링 기법을 사용하세요. )

특히, 만약 모수가 다소 다른 몇몇 하위모집단으로 나뉘어 진다면, 하위 모집단이 동일한 크기를 요구하는 층화 추출이 유용할 수 있다. 이런 방식들로, 각 부분 모집단의 단위는 무작위화 되지만, 전체 표본은 그렇지 않습니다. 그런 다음 실험 결과는 실험 단위에서 더 많은 단위 집단으로 안정적으로 일반화됩니다.

당신은 또한 결과의 표준오차 / 오차한계와 신뢰 구간의 넓이를 계산하기위해 부트스트래핑 기법을 사용할 수도 있다. 즉, 만약 A/B 테스트의 표준오차(SE) 가 크거나 신뢰구간(CI) 가 넓다면, 결과의 정확도가 낮고 결과가 전체 모집단에 적용했을 때, 일반화 되지 않을 것이라고 결론 내릴 수 있다.

유효성(Potency)

개입이 종속 변수에서 측정 가능한 변화를 생성할 수 있는 충분한 효과가 있는지 확인하는 것은 중요하며, 그렇지 않으면 개입이 효과가 없다고 잘못 가정할 수 있습니다 (유형 Ⅱ 오류). 대안적으로, 이것은 종속 변수가 반드시 처치 방법에 민감해야 된다는 것을 의미합니다. 민감도는 반복 측정을 수행하고 평균화함으로써 (e.g. Bootstrapping) 노이즈를 ( 예를 들어 측정 오류), 줄임으로써 향상될 수 있습니다.

A/B 검정의 SE가 크거나 CI가 넓은 경우 결과의 정밀도가 낮고 전체 모집단에 적용할 때 결과가 일반화되지 않는다는 결론을 내릴 수 있습니다.

A/B 테스트의 공통적인 문제와 함정

온라인 실험에 실패하지 않기 위해서, 다음의 가이드라인을 따르고 인내심을 갖고 잘 준비되고 실행된 A/B 테스트 실험으로 갔을 때 발생할 수 있는 일련의 행동들을 경험하는 것은 중요합니다. 다음은 빈번하게 발생하는 A/B 테스팅의 공통적인 문제와 함정들과 함께 상응하는 해결책들 입니다.

교란효과 (Confounding Effects)

종속변수에도 영향을 미치는 다른 알려진 모든 가능한 요인들이 일정하게 유지되도록 하는 것이 중요합니다. 따라서, 원하지 않거나 불균등한 요인 (외부 변수 라고도함)을 가능한 많이 제어해야 합니다. 외부 변수는 독립 변수와 종속 변수 모두와 연관되어 있을 때 중요합니다. 이 문제의 특별하고 극단적인 한 가지 사례는 특정한 가짜 변수를 고려할 때 독립 변수와 종속 변수 사이의 관계가 완전히 변화/반전될 때 발생하는데, 이것은 종종 심슨의 역설(Simpson's Paradox)에 의해 언급됩니다. 이러한 효과를 통제해야 하는 이유는 무작위로 처치에 단위를 할당하는 것이 교란을 완화하는 경향이 있으므로 처치 이외의 요인으로 인한 효과가 처치의 결과로 나타나기 때문입니다. 따라서 교란 효과는 A/B 실험의 내적 타당성을 위협합니다. 이 문제를 방지하기 위해 다음과 같은 해결책이 도움이 될 수 있습니다.

교란 변수의 통제
신뢰할 수 있는 기기(IV 또는 2SLS 추정)
독립변수와 종속변수의 적절한 선택
임의표본 생성

선택 편향 (Selection Bias)

A/B 테스팅의 기본적인 가정 중 하나는 당신의 표본이 비편향되었고, 모든 유저의 유형들이 동일한 확률로 샘플에 포함되었다는 것이다. 만약 몇몇 오류로 특정 모집단의 일부분이 제외 되었을 수도 있다. (예를 들어, 오직 하나의 주만을 표본으로 추출하여 미국의 평균 몸무게를 표본으로 추출한다: 마지막으로 교육에 대한 예시이다) 그러면 이것을 선택 편향이라고 부른다.

진짜 모집단 분포를 알면서 당신의 샘플이 편향되었는지 확인하기 위해, 당신의 샘플로 부터 B 부트스트랩 샘플을 만들어서 표본 평균 분포를 추출해볼 수 있다. 만약 분포가 진짜 모집단의 평균 근처러 모이지 않는다면, 당신의 샘플은 편향된 것이고, 비편향된 랜덤 샘플링을 하기 위해서 좀 더 solid 샘플링 기법들을 사용해야한다.

체계적 편향 (Systematic Bias)

이 문제는 처치의 영향을 측정하는 방법(새로운 버전의 제품 또는 기능)에 관한 것입니다. 측정할 때 체계적으로 오류를 범하고 있나요? 측정 값이 매번 동일한 방식으로 측정되므로 이러한 유형의 오차는 항상 동일한 양 또는 동일한 비율로 측정값에 영향을 미치기 때문에 예측이 가능합니다. 추정 결과의 정밀도에 주로 영향을 미치는 무작위 오차와는 달리, 체계적인 오차는 결과의 정확도에 영향을 미칩니다.

조기 중단 (Early Stopping) or P-hacking

A/B 실험의 일반적인 실수는 통계적으로 유의한 결과(예: 작은 p-값)를 관찰한 후 조기에 실험을 중지하는 것이며, 유의 수준 및 다른 모든 모델 매개변수는 A/B 테스트의 Power Analysis 단계에서 미리 결정되고 최소 표본 크기가 달성될 때까지 실험이 실행된다고 가정하는 것입니다.

P-해킹 또는 조기 중단은 결과의 내적 타당성에 영향을 미치고 편향되게 만들며 오탐을 유발하기도 합니다.

여파 또는 네트워크 효과 (Spillover or Network Effects)

이 문제는 보통 A/B 테스트가 페이스북, 인스타그램, 틱톡과 같은 소셜 미디어 플랫폼뿐만 아니라 연결된 실험 및 통제 그룹의 사용자가 같은 그룹 또는 커뮤니티에 있고 실험 및 통제 제품 버전에 대한 서로의 반응에 영향을 미치는 다른 제품에서도 발생합니다. 이 문제는 시험 및 통제 효과의 무결성을 침해하므로 편향된 결과와 잘못된 결론을 초래합니다.

네트워크 효과를 탐지하려면 계층화 샘플링을 수행한 다음 이를 두 그룹으로 나눌 수 있습니다. 그런 다음 군집화된 표본을 고려하여 한 표본에 대해 A/B 검정을 실행할 수 있고 그렇지 않은 표본에 대해 A/B 검정을 실행할 수 있습니다. 처치 효과에 차이가 있으면 네트워크 효과 문제가 있다고 볼 수 있습니다.

변화에 대한 반감과 참신성 효과 (Change Aversion and Novelty Effects)

당신이, 제품의 변화가 유의미한지 테스트하고자 할때, 사용자는 원하지 않더라도, 처음 사용자는 기능이 통제군/현재 버전 보다 실제로 더 낫지 않지만 궁금함에 그냥 시도해볼 지도 모른다. 이것을 참신성 효과 (Novelty Effects) 라고 부르며, 이것은 결과의 내부적 타당성에 영향을 줍니다. 게다가 새로운 기능 (실험 제품 버전)은 또한 몇몇 유저가 이 새로운 버전을 싫어하여 이탈하게 되는 전체 유저의 경험에 영향을 줄 지도 모릅니다. 이 현상을 변화에 대한 반감 (Change Aversion) 이라고 합니다.

참신성 효과를 확인하고자 사용되는 가장 유명한 방법중 하나는 유저를 신규 vs 기존 유저로 세그먼팅하는 것입니다. 만약 기능이 복귀 유저들에 의해 선호되지만, 새로운 유저들에게는 그렇지 않다면, 대부분 참신성 효과를 다루고 있을 가능성이 높습니다.

표본 비율 불일치 (Sample Ratio Mismatch)

만약 통제군과 실험군 사이의 분할이 의심스러워 보인다면, 즉 처치 할당 프로세스가 더 많은 유저들이 실험군/통제군 그룹보다 통제군/실험군 그룹에 할당 되는 것처럼 생각이 된다면, Chi-square test를 수행해볼 수 있습니다.
이 테스트는 표본 비율 불일치를 공식적으로 확인하는 데 도움이 됩니다. 이 테스트에 대한 자세한 내용은 여기에서 확인할 수 있습니다.

부적절한 테스트 기간 선택 (Inadequate Choice of Test Period)

A/B 테스팅에서 또다른 흔한 실수는 테스트 기간의 선택에 있습니다. 위에서 말했듯이, A/B 테스팅의 기본적인 가정중 하나는 모든 유저의 유형들이 동등한 확률로 표본에 포함되었다는 것을 가정합니다. 그러나 휴일, 계절성, 주말 및 기타 관련 이벤트를 고려하지 않은 기간에 테스트를 실행하면 다양한 유형의 사용자가 선택될 확률이 더 이상 동일하지 않습니다(예: 주말 쇼핑객, 휴일 쇼핑객 등). 예를 들어, 테스트를 일요일 아침에 수행하는 것은 똑같은 테스트를 화요일 오후 11시에 수행하는 것과 다를 것입니다.

너무 많은 테스트를 동시에 수행하는 것 (Running too many tests at the same time)

두 가지 이상의 변형이 나타나는 멀티태스킹을 위해 테스트하려는 제품에 두 가지 이상의 실험 변형이 있는 경우에는 더 이상 동일한 유의 수준을 사용하여 통계적 유의성을 테스트할 수 없습니다. 따라서 결과를 비교할 p-value 또는 유의수준을 조정할 필요가 있습니다.

이런 경우, Bonferoni 상관계수를 사용하여, 표본 갯수 n 에 기반한 신뢰 수준을 조정할 수 있습니다. 그래서, 다항변수 테스팅에 사용되는 신뢰 수준은 alpha/N 이 되어야 합니다. 예를 들어, 만약 신뢰 수준이 5% 라면 새롭게 조정된 신뢰 수준은 0.05/n 이 되어야합니다.

최신성 효과를 확인하는 가장 유명한 방법 중하나는 유저를 기존 vs 신규로 나누는 것입니다. 만약 기능이 복귀 유저들에 의하여 선호가 되나, 신규 유저에는 그렇지 않다면, 참신성 효과를 다루고 있다고 볼 수 있습니다.

A/B 테스팅의 윤리와 프라이버시 (Ethics and Privacy In A/B testing)

A/B 테스팅가 유명해지면서, A/B 테스팅에 대한 프라이버시와 윤리에 대한 염려도 생기고 있다. 즉, 다음 질문에 ㄷ
즉, 다음과 같은 질문이 도움이 됩니다.

사용자에게 조건 및 위험에 대한 정보를 제공합니까?
데이터에 첨부된 사용자 식별자는 무엇입니까?
어떤 형태의 데이터를 수집합니까? (개인적, 자발적 동의)
테스트 및 수집된 데이터의 기밀성 및 보안 수준은 어느 정도입니까, 모두 알고 있습니까?

A/B 실험을 수행할 때 한 세트의 사용자에게 제공(실험)하고 다른 샘플의 사용자에게 제공하지 않을 때 처치(더 나은 제품/더 나은 기능)의 사용자의 권한을 제거하지 않도록 하기를 원한다. 게다가, 고려해야 할 다른 문제들은 사용자가 가질 수 있는 다른 대체 서비스들이 무엇인지, 그리고 시간, 돈, 정보 등의 측면에서 스위칭 비용이 얼마인지에 관한 것이다. 예를 들어, 검색 엔진의 변경 사항을 테스트하는 경우 참가자는 항상 다른 검색 엔진을 사용할 수 있습니다. 주요 쟁점은 참가자들이 선택할 수 있는 대안이 적을수록 강제성을 둘러싼 문제가 발생하고, 참가자들이 실제로 참가 여부에 대한 선택권이 있는지, 이것이 위험과 이익에 대해 어떻게 균형을 이루는지에 대한 문제입니다.

https://playinpap.github.io/bayesian-abtest/

베이지안 A/B 테스트 in Python

베이지안 관점에서 AB Test를 하는 방법에 대해 정리했습니다. 전체 코드는 여기 에서 확인할 수 …

playinpap.github.io

https://github.com/intercom/expan-intercom

GitHub - intercom/expan-intercom: A/B testing library for Python

A/B testing library for Python. Contribute to intercom/expan-intercom development by creating an account on GitHub.

github.com

https://blog.naver.com/plasticcode/222620878854

AB 테스트는 무엇이고 어떻게 해야 잘 할 수 있을까?(전환율 예시)

AB 테스트가 무엇이고 이걸 어떻게 잘 할 수 있는지를 살펴보려고 한다. AB 테스트는 A랑 B 중에 무...

blog.naver.com

https://towardsdatascience.com/a-b-testing-with-chi-squared-test-to-maximize-conversions-and-ctrs-6599271a2c31